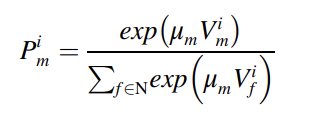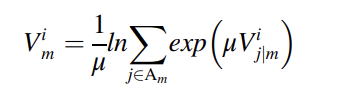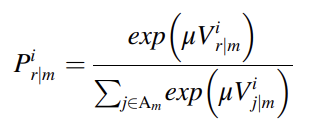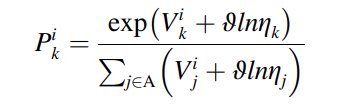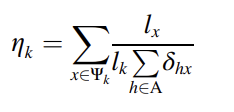Demand-responsive passenger flow control strategies for metro networks considering service fairness and passengers’ behavioural responses

论文题目:Demand-responsive passenger flow control strategies for metro networks considering service fairness and passengers’ behavioural responses
论文作者:郇宁,姚恩建,张金萌
论文期刊:Transportation Research Part C
网址:https://doi.org/10.1016/j.trc.2021.103335
关键词:运营管理,进站流控制,MPEC,出发时间选择,方式转移,随机用户均衡
1摘要
本文介绍了一种为过饱和地铁网络制定的需求响应型客流控制策略方法,并进行了一项 "陈述偏好-隐藏偏好融合"(SP-off-RP)的调查,以获取乘客对客流控制策略的行为选择结果,结果显示乘客在出发时间和方式选择方面有明显的行为变化意向,目前,这种行为反应往往被忽视,导致在估计目标群体规模和提出策略的表现时出现偏差。为了解决这个问题,本文开发了一种带有平衡约束的数学规划(MPEC)方法来优化需求响应型客流控制策略。提出的MPEC模型强调平衡地铁系统的运营效率和乘客感知的服务公平性。另外,提出基于巢式Logit的随机用户均衡问题以适应候选客流控制策略所驱动的潜在需求模式变化,基于广州和北京地铁的两个案例被用来证明所提出的模型和解决方案的有效性。强调服务公平和乘客出行行为有助于为地铁运营商和乘客创造一个双赢的局面。在广州和北京的地铁中,在最佳客流控制策略下,最高路段的负荷率分别从126.6%和122.98%下降到105.7%和106.87%。相应的网络负荷基尼系数分别从0.278和0.269提高到0.259和0.248,显示了这种方法在削峰和平衡负荷方面的显著表现。
2引言
随着人们对促进城市地区可持续交通的日益关注,城市轨道交通已被认为是通勤者最值得推荐的公共交通出行方式。由于地铁相对于其他出行方式具有出色的准时性,因此被长途通勤者所青睐。在过去十年的地铁网络快速扩张中,全球大多数新兴的大型地铁网络都面临着过饱和的运营状况,在高峰期尤为明显(Liu等人,2019)。以广州地铁为例,截至2020年12月,总运营里程达到553.2公里,位列全球第四大系统。如图1所示,由于地铁网络的不断扩张,2019年日均乘客量超过了900万人次。
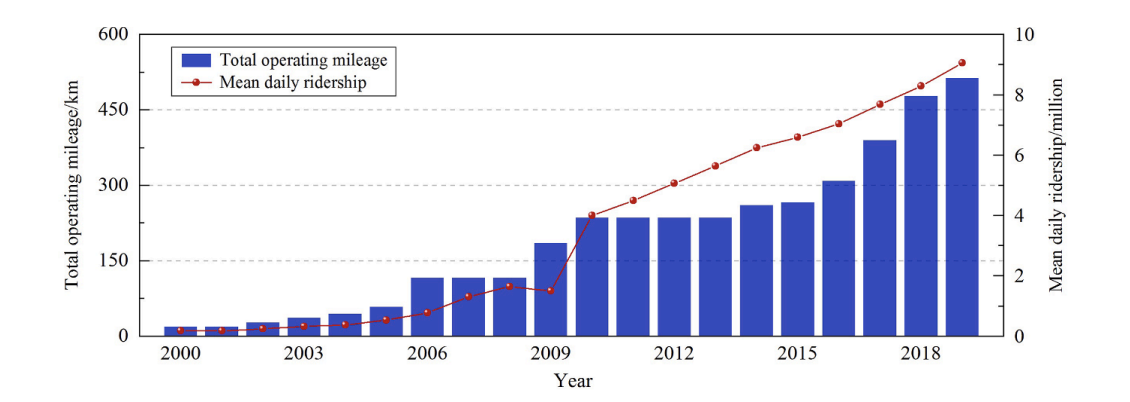
图 1 运营里程和日均客流变化
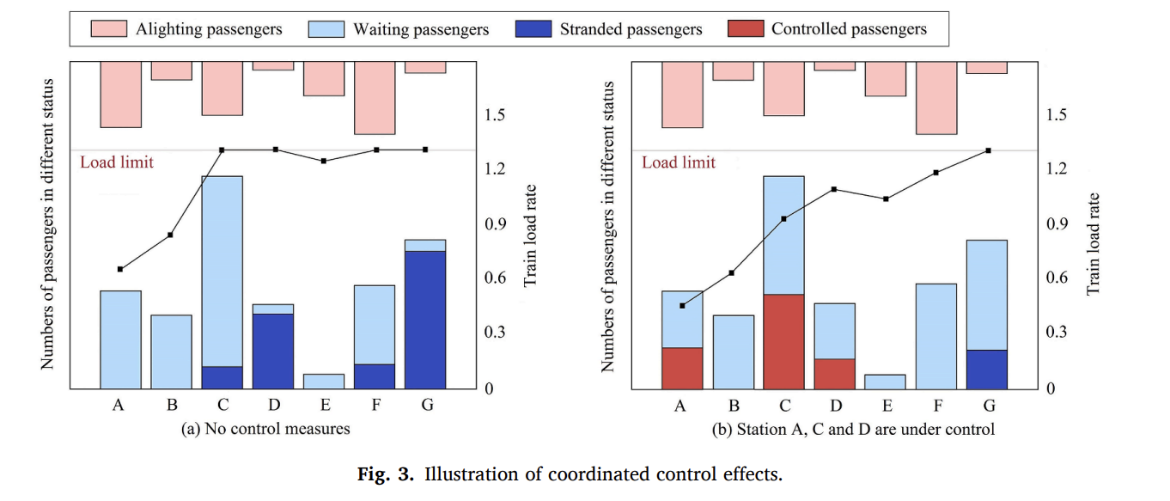
图 2 协调控制效果实例
图2通过两个例子来证明协调控制策略的重要性,其中图2(a)和图2(b)有 相同的客流需求设置,即在平台上等待上车的乘客数量相同。与图2(a)相比,图2(b)中使用了客流控制措施;即A、C、D站处于控制之下,因此被控制的客流数量不同。此外,通过比较这两个例子,列车负载率可以用来识别客流控制的效果,当没有采取控制措施时,D站和G站几乎被滞留的乘客堵住,因为到达的列车在离开C站后已经满员。然而,如果A、C、D三站同时被控制,列车载客率的上升就会有效减缓,这表明列车的运力在最后一个车站G之前仍然充足。这使得有限的运力能够在各站之间合理分配,从而避免了某些车站的乘客遭遇如图2(a)中所示的超长的延误。为此,本文采用协调设计来制定客流控制策略,在优化问题中,所有的车站都由列车的运行程序和乘客的换乘行为联系起来。
除了协调控制设计外,在相关研究中(Jiang等人,2017)运营效率也被认为是一个主要优化目标。然而,伴随而来的服务公平问题在过去的工作中却很少被讨论,特别是关于平衡不同车站的乘客延误,这种对公平性考虑的缺失很容易在不同程度上导致乘客出行体验的降低,甚至导致乘客对地铁服务的忠诚度下降。此外,很少有人关注乘客对执行客流控制的行为响应,进一步限制了现有理论方法的可行性。因此,在本研究中,采用了带有平衡约束的数学规划方法(MPEC)来制定需求响应型客流控制策略,同时考虑到服务的公平性和乘客的行为变化意图。
3乘客行为选择模型
在这项研究中,基于在中国广州进行的SP-off-RP的调查,利用收集到的SP数据,在巢式Logit(NL)结构的基础上,对乘客的出发时间和方式转移决策进行建模,该模型反映了由客流控制策略驱动的需求模式。此外,使用路径选择模型(PSL)对所收集的RP数据模拟乘客的路径选择行为,该模型被用来获得MPEC问题中换乘站的换乘需求模式。
3.1数据调查
一般来说,即使在客流控制的情况下,乘客也会在最小程度上调整他们出行行为。本文假设,只有当乘客决定继续乘坐地铁时,才会产生出发时间的改变;也就是说,出发时间的改变不会与出行方式的改变同时发生。在离散选择模型中,受访者的选择通常被定义为决策者的备选项。在本研究中,我们用 "A "来表示备选方案的集合,如图4所示。每个SP选择任务,A中有六个元素,分别是不改变方式和提前出发(A1),不改变方式和不改变出发时间 (A2),不改变方式和晚点出发(A3),改乘公共汽车和不改变出发时间(A4),改乘私家车和不改变出发时间 (A5),以及转向出租车或电子叫车和不改变出发时间(A6)。鉴于各替代方案之间存在关联性,特别是对于三个与地铁相关的替代方案,本文使用了一个NL结构来模拟乘客的出发时间和方式转换决定,并将替代方案归入相互排斥的巢穴。本文用'N'来表示巢穴的集合,采用两个巢穴以说明联合选择行为。
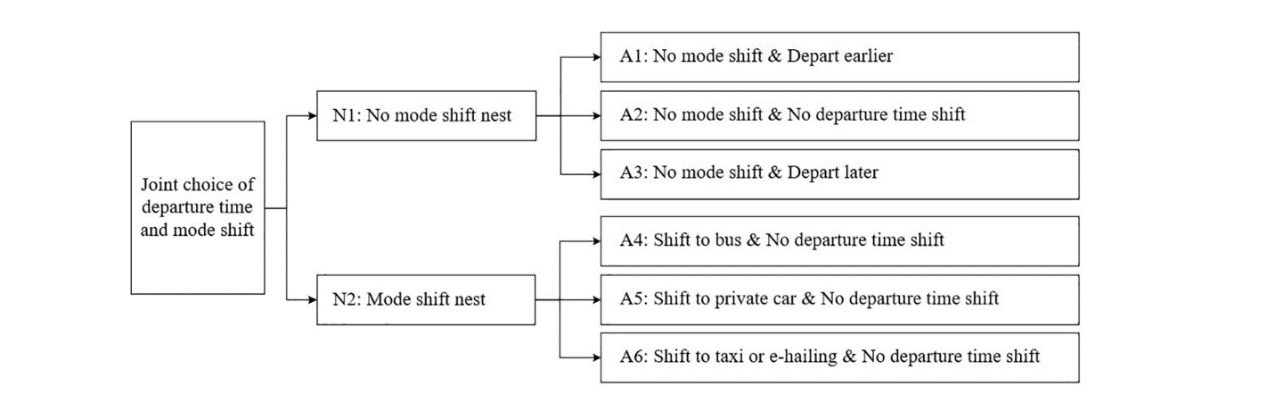
图 3 巢式Logit模型结构
关于属性的设置,六个备选方案的出发地-目的地对(O-Ds)与先前在RP部分回答的受访者相同。因此,不同出行方式的服务水平(LOS)属性与实际决策环境一致。根据受访者自己的O-Ds,不同出行方式的服务水平(LOS)属性与真实的决策环境一致。除了可以直接从受访者的RP回答中收集到地铁的LOS属性外,公交车、私家车、出租车和网约车方式的LOS属性在百度地图导航应用程序接口(API)的辅助下也得到了补充。此外,我们还引入了几个情景属性,以反映客流控制策略对当前地铁服务的影响。表1列出了NL模型中使用的属性。
表 1 NL模型中考虑的属性
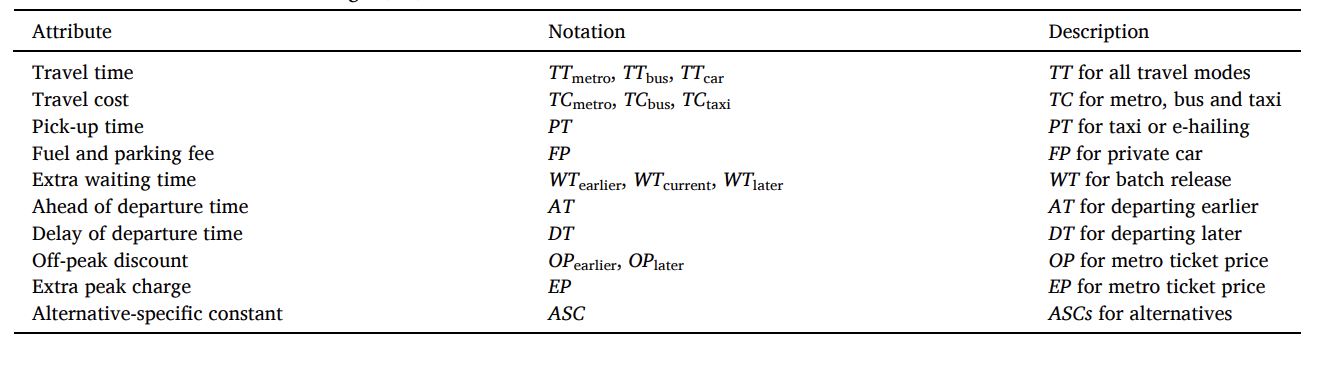
图4展示了RP组成和SP选择任务的一个例子。通过在线调查,本文在2019年5月收集了1015份问卷。根据收集到的RP信息,考虑到地铁通勤乘客应该清楚他们的日常通勤行程细节,本文设计了逻辑一致性测试来过滤不合格的受访者。例如,如果受访者自报的票价与官方公布的价格不一致,他/她就不被认为是地铁通勤乘客,则从样本集中剔除。本次调查最终获得了796个有效问卷,共涉及2388个SP选择结果,这些结果被用来估计出发时间和方式联合选择模型。此外,收集到的RP信息中的路径细节被用来标定路径选择模型。
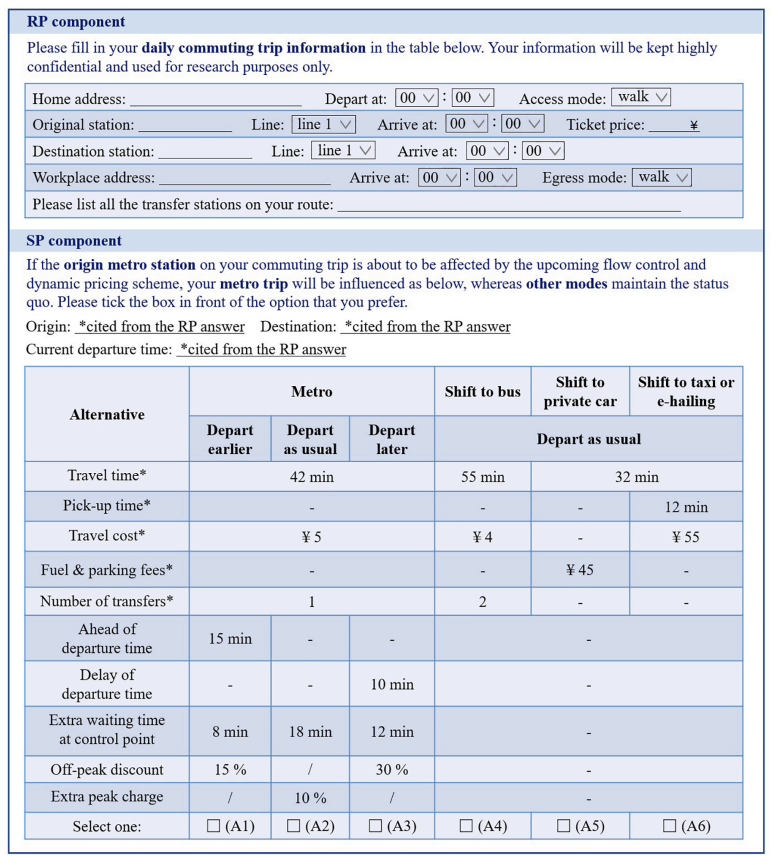
图 4 问卷中RP与SP调查组成部分实例
3.2出发时间和方式选择的NL模型
根据收集到的SP实验调查结果,本文使用NL结构来模拟乘客对实施客流控制策略的选择行为。在NL模型中,对于乘客i,我们用Pi 来表示在巢穴m中选择备选方案r的概率,如下所示。
|
| (1) |
式中为选择巢m的边际概率,为选择巢m中备选项r的条件概率。计算和方法如下。
|
| (2) |
|
| (3) |
|
| (4) |
本文使用NL模型中A1-A6的效用函数如下:
|
| (5) |
|
| (6) |
|
| (7) |
|
| (8) |
|
| (9) |
|
| (10) |
本文NL模型使用Python Biogeme进行标定,Biogeme是为离散选择模型而开发的开源软件(Bierlaire,2016)。为了确保标定的NL模型可以用来预测MPEC问题中的需求模式变化,没有使用社会人口经济变量。NL模型的标定结果见表2。
表 2 NL模型标定结果
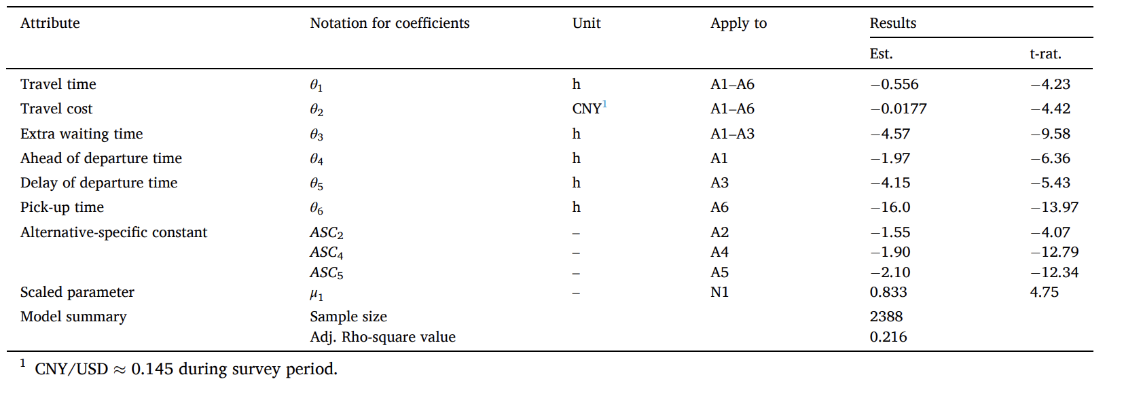
表2中的参数标定结果都显示出显著的t值,其绝对值高于1.96。除了出行行时间和出行费用这些最常用的LOS属性外,受客流控制策略的影响,乘客对等待时间(WT)表现出强烈的敏感性。此外,较高的提前出发时间(AT)或延迟出发时间(DT)值分别导致了对A1和A3选择的负面影响。A2的方案常数项标定结果为负意味着乘客倾向于通过转移到A1或A3来重新安排出发时间,而不是在A2承受相对较长的延误。同样,A4和A5的方案常数项标定结果为负表明,退出地铁的乘客更愿意转乘出租车或网约车,而不是公交车和私家车。对于A6,出租车或网约车服务的等待时间对乘客的感知效用产生了负面影响。此外,N2的比例参数塌陷为1,表明A4、A5和A6的多项式Logit(MNL)结构。
总的来说,调整后的Rho-square值大于0.2,代表模型拟合效果良好,这意味着NL模型具有足够的解释力,可以支持在MPEC问题上进一步应用基于NL的随机用户平衡(NL-SUE)。
3.3路径选择的PSL模型
除了NL模型外,本文使用受访者的RP路径选择观察标定了PSL模型,以估计换乘站的换乘需求模式,以帮助提供优化客流控制策略的必要输入数据。使用PSL模型的原因是为了解决MNL模型中无关选项的独立性问题(IIA特性)。本文用来表示捕捉路径的不同路径选择之间的相关性的修正项(Prato等人,2012)。对于通勤者i,选择路径k的概率如下:
|
| (11) |
|
| (12) |
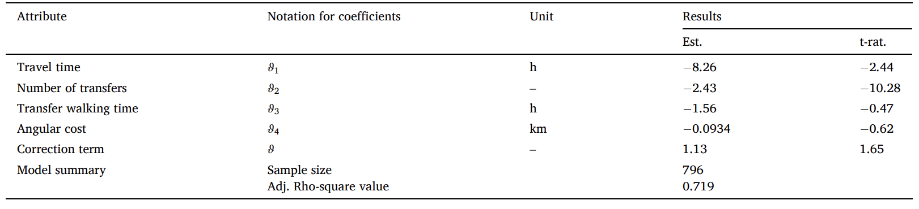
PSL模型标定结果如表3所示:
表 3 PSL模型标定结果
4优化客流控制策略的MPEC模型构建
本章介绍了优化客流控制策略的MPEC模型,其目的是为了提高轨道交通系统运营效率和服务的公平性,其中,NL-SUE约束被考虑用来预测由客流控制策略驱动的需求模式。为了支持目标函数的计算,图5给出了建立的流量传播的框架。

图 5 城轨系统中流量传播框架构建
本文构建的MPEC问题是一个具有高计算复杂性的NP-hard问题。因此,采用基于遗传算法(GA)的连续加权平均法(MSWA)算法进行模型求解。图6显示了基于遗传算法的MSWA求解算法流程图。
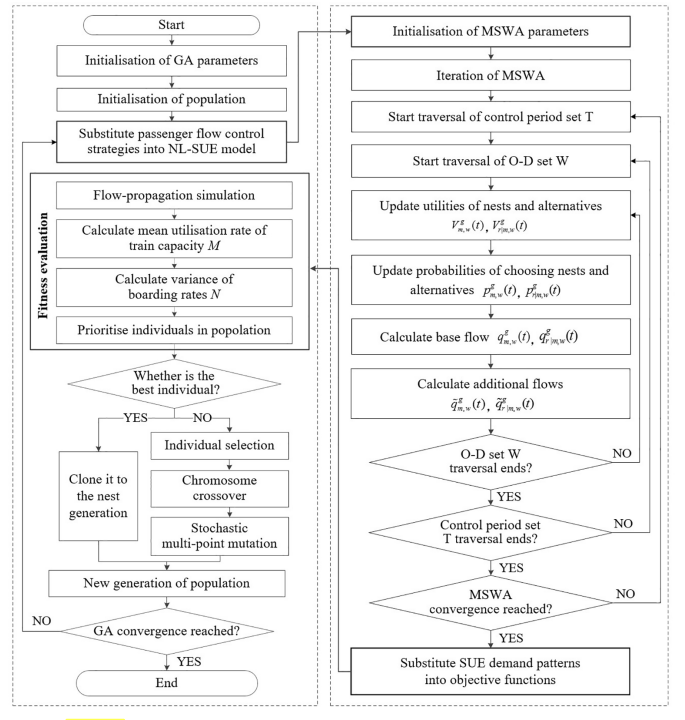
图 6 基于遗传算的连续加权平均法求解算法流程图
5广州与北京地铁实例分析
基于所提出的MPEC模型,本文进行了一项实证案例研究,提出真实环境中的需求响应型客流控制策略,以适应现实世界的需要。
图7为北京和广州的局部轨道交通网络,本文将其作为基础进行研究。网络(a)位于广州西部,本文选择1、5、6号线的西行方向和2号线的南行方向来把握从郊区到市中心的通勤客流。网络(b)位于北京北部,本文选择5号线和8号线的北行方向,昌平线、13号线的顺时针方向来研究客流控制问题。值得注意的是,由于调查只在广州进行,广州和北京地铁的案例研究都使用了在广州收集的样本所标定的选择模型,本文假设广州乘客和北京乘客的行为是相同的,两个城市的乘客在时间价值上可能会有轻微的偏差。本文以北京地铁为例,展示了所提出的MPEC模型的可重复使用性。
本文基于IC刷卡数据和实际列车时刻表,首先使用标定的PSL模型得出两个局部网络的当前需求模式,并作为优化模型的输入数据,如表4所示。
表 4 两个轨道交通网络中当前需求模式示例
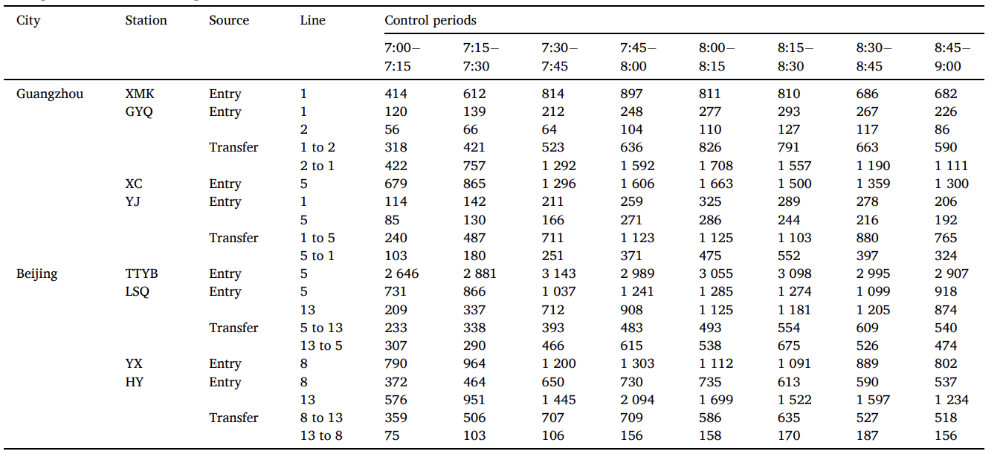
使用本文提出的模型对两个城市分别进行客流控制策略优化,本文使用了两个目标,即列车运力的平均利用率(UR-TC)和上车率的方差(V-BR)来评估不同决策偏好下的优化策略的性能,如表5所示。
表 5 北京和广州模型表现对比
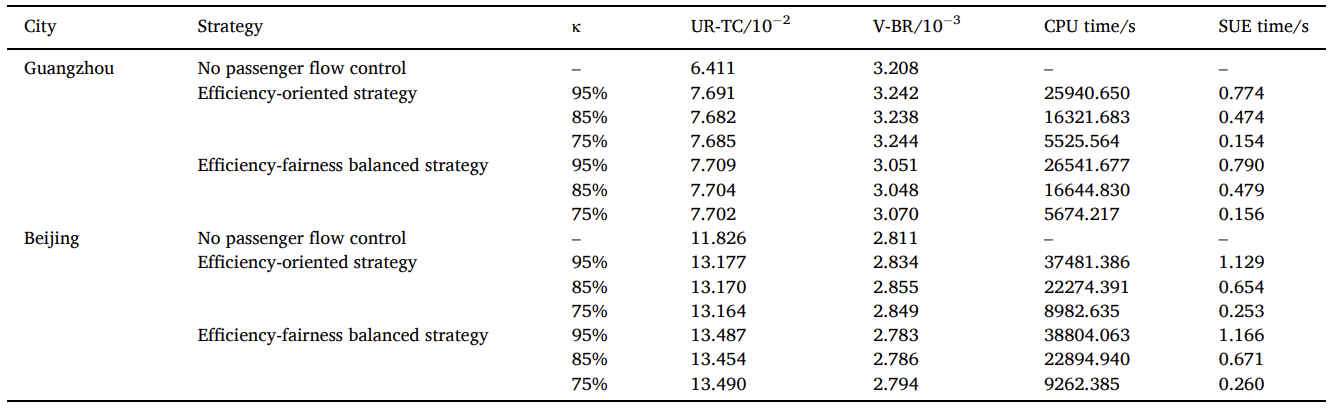
对于每个城市,本文以 "无客流控制"(策略1)为参考,并与传统的以效率为导向的客流控制策略(策略2)和效率-公平均衡的客流控制策略(策略3)进行比较。相对于策略1,策略2增加了两个城市的UR-TC和V-BR,这表明运营效率有所提高,但服务公平性有所损失。相比之下,策略3在UR-TC和V-BR方面都优于策略2,体现了公平性的考虑与效率的追求并不冲突,而且有助于实现地铁运营商和乘客的双赢。总的来说,北京的UR-TC比广州的高。北京的上车率在时间和空间上的分布都比广州的要均匀。CPU时间和SUE时间列于表5。
策略3(κ=95%)的最优解以逐站时间序列形式呈现,如图7所示。此外,这两种最佳策略的效果是根据路段负荷率(SLR)来评估的。在实践中,SLR是量化地铁线路拥挤程度的一个常用指标,它反映了一段时间内通过目标区段的列车的整体负荷状况。一般来说,当SLR高于0.8时,乘客的感知舒适度会变差,当SLR超过1.0时,列车车厢就会变得过于拥挤。
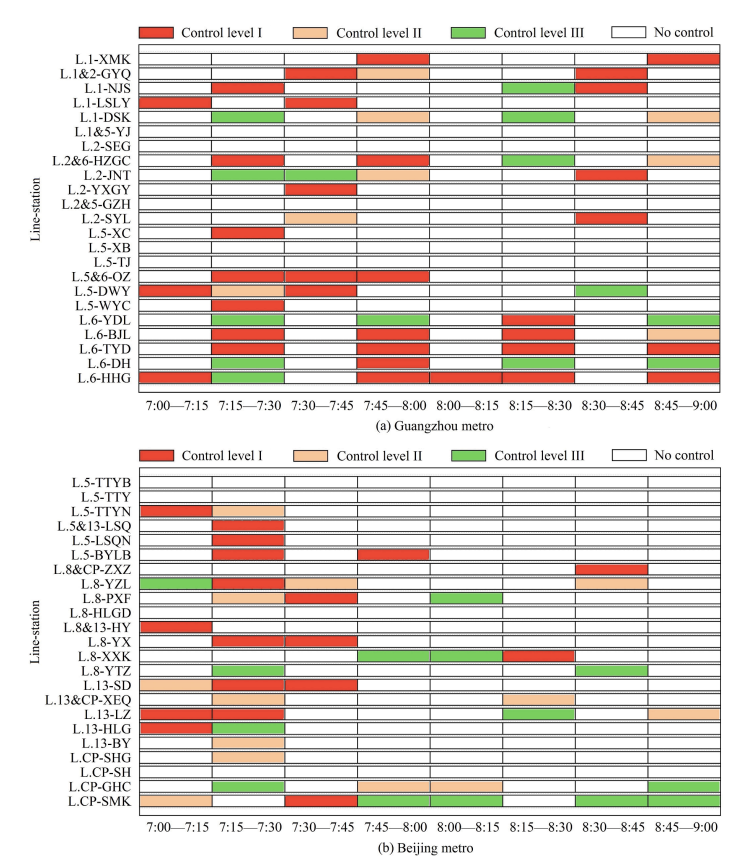
图 7 北京和广州地铁优化客流控制措施
图8比较了在两个地铁网络中实施客流控制策略前后的SLRs的时空分布,在广州地铁的现状下(优化前),5号线和6号线的SLRs相对高于其他两条线路,特别是在早上8点到8点30分;相比之下,北京地铁的高峰期开始得更早,特别是5号线和CP线,LSQ-LSQN和LSQN-BYLB的路段在所有控制期间都非常拥挤。经过优化,拥挤现象得到了有效的缓解,在时间和空间上都呈现出更均匀的负荷分布模式。
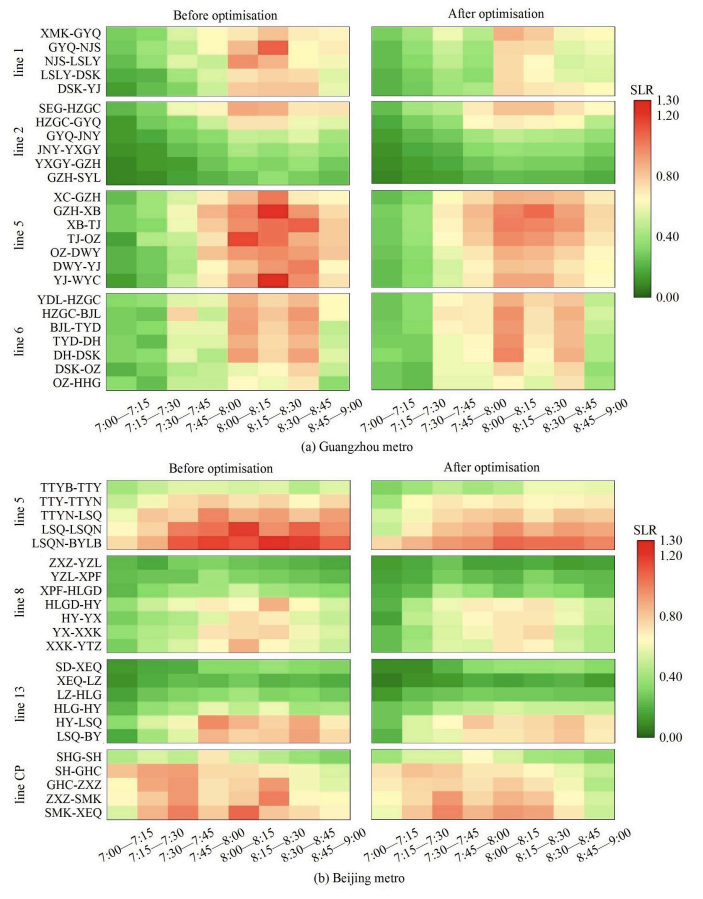
图 8 优化前后路段载荷时空分布情况
表 6优化前后前十拥挤路段及SLR值
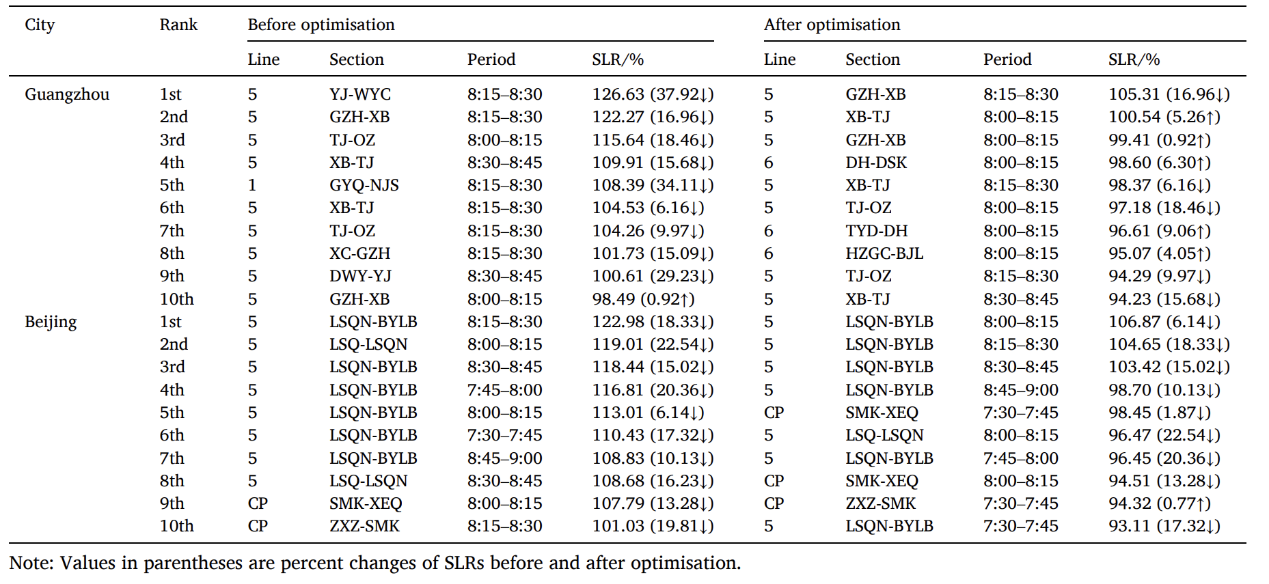
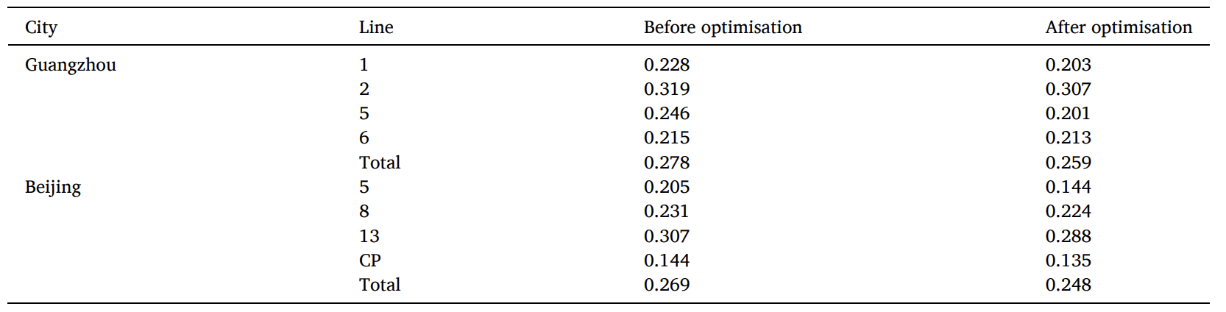
表6总结了两个城市优化前后的前10拥堵路段及SLR值。优化前,两个网络的最高SLR在8:15-8:30期间,位于YJ-WYC和LSQN-BYLB的路段上,分别达到126.63%和122.98%。经过优化后,这两个路段的SLR分别下降到105.31%和106.87%,显示了提出策略的显著削峰效果,客流控制策略在一定程度上激发了乘客的避峰行为。SLR的空间分布显示出微妙的变化,因为拥挤部分转移到了相邻的路段。本文进一步测量了 SLRs的基尼系数,以评估网络的负荷状态(Huang等人,2018)。一般来说,基尼系数的数值越低,表明网络负载越平衡。正如在表7所示,对于广州和北京的地铁线路,负载比优化前情况更加平衡。 广州地铁的网络负荷基尼系数从0.278下降到0.259,北京地铁的网络负荷基尼系数从0.269下降到0.248,这表明提出的策略具有不错的平衡负荷效果。
表 7网络基尼系数结果
6结论
本文提出了一种有效的方法来优化需求响应型的客流控制策略,利用NL模型深入研究了乘客对客流控制策略的行为选择,应用MPEC问题,将需求模式的变化纳入客流控制策略的制定中。
从这项工作中可以得出几个结论,概述如下。
根据在中国广州进行的SP-off-RP调查,地铁乘客对客流控制措施造成的延误表现出更强的敏感性,对客流控制措施造成的延误的敏感度高于正常的出行时间,这促进了乘客在出发时间和方式选择方面的行为变化。另外,制定兼顾效率和公平的客流控制策略对保持乘客量至关重要,这也是本文提出的方法的主要贡献。
本研究与以往的研究不同,以往的研究只注重提高运营效率,而忽略了乘客对服务公平性的感知和乘客的行为因素。对两个城市的地铁网络进行的案例研究结果表明,传统的以效率为导向的模式加剧了乘客延误的不平衡性,从而在一定程度上损害了服务的公平性。相比之下,所提出的效率-公平均衡模型达到了更好的运营效率,这主要受益于协调控制效应,并证明了纳入公平考虑与提高运营效率并不冲突。在广州和北京地铁采用最优客流控制策略后,最高的SLRs从126.63%、122.98%分别下降到105.5%、106.87。网络负荷的基尼系数分别从0.278、0.269降至0.259、0.248,这显示出应对高峰期拥挤时具有相当大的削峰和负载平衡效应。
从现实的角度来看,涉及到过多的车站或变化客流控制策略很难适用于大规模的地铁网络。在未来的工作中,应该进一步研究实施客流控制措施的人力成本,并在优化模型中加以说明,其形式可以是构成目标函数的一部分或预算约束。总的来说,所提出的方法能够使地铁运营商在运营管理中精确和适当地实施客流控制措施。本文对乘客行为和地铁系统中客流传播过程进行深入剖析,也为需求预测、列车调度和相关运营管理问题的研究提供了宝贵的参考。
7参考文献
Bekhor, S., Toledo, T., Reznikova, L., 2009. A path-based algorithm for the cross-nested logit stochastic user equilibrium traffic assignment. Comput. Civ. Infrastruct.Eng. 24, 15–25. https://doi.org/10.1111/j.1467-8667.2008.00563.x.
Bierlaire, M, 2016. Pythonbiogeme: a short Introduction. Report TRANSP-OR 160706. Series on Biogeme, Transport and Mobility Laboratory.
Calastri, C., Borghesi, S., Fagiolo, G., 2019. How do people choose their commuting mode? An evolutionary approach to travel choices. Econ. Polit. 36 (3), 887–912.https://doi.org/10.1007/s40888-018-0099-1.
DeSalvo, J.S., Huq, M., 2005. Mode choice, commuting cost, and urban household behavior. J. Reg. Sci. 45 (3), 493–517. https://doi.org/10.1111/jors.2005.45.issue-310.1111/j.0022-4146.2005.00381.x.
Ding, C., Mishra, S., Lin, Y., Xie, B., 2015. Cross-nested joint model of travel mode and departure time choice for urban commuting trips: Case study in Maryland-Washington. DC Region. J. Urban Plan. Dev. 141 (4), 04014036. https://doi.org/10.1061/(ASCE)UP.1943-5444.0000238.
Gentile, G., 2018. New formulations of the stochastic user equilibrium with logit route choice as an extension of the deterministic model. Transp. Sci. 52 (6),1531–1547. https://doi.org/10.1287/trsc.2018.0839.
Gu, W., Yu, J., Ji, Y., Zheng, Y., Zhang, H.M., 2018. Plan-based flexible bus bridging operation strategy. Transp. Res. Part C Emerg. Technol. 91, 209–229. https://doi.org/10.1016/j.trc.2018.03.015.
Guevara, C.A., Hess, S., 2019. A control-function approach to correct for endogeneity in discrete choice models estimated on SP-off-RP data and contrasts with an earlier FIML approach by Train & Wilson. Transp. Res. Part B Methodol. 123, 224–239. https://doi.org/10.1016/j.trb.2019.03.022.
Hensher, D.A., Rose, J.M., Collins, A.T., 2011. Identifying commuter preferences for existing modes and a proposed Metro in Sydney, Australia with special reference to crowding. Public Transp. 3 (2), 109–147. https://doi.org/10.1007/s12469-010-0035-4.
Hsu, C., Guo, S., 2006. CBD oriented commuters’ mode and residential location choices in an urban area with surface streets and rail transit lines. J. Urban Plan. Dev.132 (4), 235–246. https://doi.org/10.1061/(ASCE)0733-9488(2006)132:4(235).
Huang, Z.Y., Xu, R.H., Yang, R.D., Liu, W., 2018. Evaluation on equilibrium of passenger flow distribution on urban rail transit network. J. Transp. Syst. Eng. Inf. Technol. 18, 139–145. https://doi.org/10.16097/j.cnki.1009-6744.2018.03.022.
Jiang, M., Li, H., Xu, X., Xu, S., Miao, J., 2017. Metro passenger flow control with station-to-station cooperation based on stop-skipping and boarding limiting. J. Cent. South Univ. 24 (1), 236–244. https://doi.org/10.1007/s11771-017-3424-x.
Jiang, Z., Fan, W., Liu, W., Zhu, B., Gu, J., 2018. Reinforcement learning approach for coordinated passenger inflow control of urban rail transit in peak hours. Transp. Res. Part C Emerg. Technol. 88, 1–16. https://doi.org/10.1016/j.trc.2018.01.008.
Li, S., Dessouky, M.M., Yang, L., Gao, Z., 2017. Joint optimal train regulation and passenger flow control strategy for high-frequency metro lines. Transp. Res. Part B Methodol. 99, 113–137. https://doi.org/10.1016/j.trb.2017.01.010.
Liu, R., Li, S., Yang, L., 2020. Collaborative optimization for metro train scheduling and train connections combined with passenger flow control strategy. Omega (United Kingdom) 90, 101990. https://doi.org/10.1016/j.omega.2018.10.020.
Liu, S., Yao, E., Li, B., 2019. Exploring urban rail transit station-level ridership growth with network expansion. Transp. Res. Part D Transp. Environ. 73, 391–402. https://doi.org/10.1016/j.trd.2018.04.006.
Lo, H.K., Yip, C.-W., Wan, Q.K., 2004. Modeling competitive multi-modal transit services: A nested logit approach. Transp. Res. Part C Emerg. Technol. 12 (3-4), 251–272. https://doi.org/10.1016/j.trc.2004.07.011.
Nian, G., Chen, F., Li, Z., Zhu, Y.i., Sun, D.(., 2019. Evaluating the alignment of new metro line considering network vulnerability with passenger ridership. Transp. A Transp. Sci. 15 (2), 1402–1418. https://doi.org/10.1080/23249935.2019.1599080.
Nurul Habib, K.M., 2012. Modeling commuting mode choice jointly with work start time and work duration. Transp. Res. Part A Policy Pract. 46 (1), 33–47. https://doi.org/10.1016/j.tra.2011.09.012.
Prashker, J.N., Bekhor, S., 2004. Route choice models used in the stochastic user equilibrium problem: A review. Transp. Rev. 24, 437–463. Doi: 10.1080/0144164042000181707.
Prato, C.G., Bekhor, S., Pronello, C., 2012. Latent variables and route choice behavior. Transportation (Amst). 39 (2), 299–319. https://doi.org/10.1007/s11116-011-9344-y.
Qi, J., Yang, L., Di, Z., Li, S., Yang, K., Gao, Y., 2018. Integrated optimization for train operation zone and stop plan with passenger distributions. Transp. Res. Part E Logist. Transp. Rev. 109, 151–173. https://doi.org/10.1016/j.tre.2017.11.003.
Resdiansyah, Munawar, A., Suryo Putranto, L., Zhang, J., Shah, M.Z., Sutandi, A.C., Prasetijo, J., Hario Setiadji, B., Isran Ramli, M., Asad Abdurrahman, M., 2018. Travel mode choice preferences of urban commuters in Kuching City, Malaysia based on stated preference data. MATEC Web Conf. 181, 02007. https://doi.org/10.1051/matecconf/201818102007.
Roby, H., 2014. A Supplementary Dictionary of Transport Studies, in: A Supplementary Dictionary of Transport Studies. Oxford University Press. Doi: 10.1093/acref/9780191765094.001.0001.
Sasic, A., Habib, K.N., 2013. Modelling departure time choices by a Heteroskedastic Generalized Logit (Het-GenL) model: An investigation on home-based commuting trips in the Greater Toronto and Hamilton Area (GTHA). Transp. Res. Part A Policy Pract. 50, 15–32. https://doi.org/10.1016/j.tra.2013.01.028.
Shi, J., Yang, L., Yang, J., Zhou, F., Gao, Z., 2019. Cooperative passenger flow control in an oversaturated metro network with operational risk thresholds. Transp. Res. Part C Emerg. Technol. 107, 301–336. https://doi.org/10.1016/j.trc.2019.08.008.
Train, K.E., Wilson, W.W., 2009. Monte Carlo analysis of SP-off-RP data. J. Choice Model. 2 (1), 101–117. https://doi.org/10.1016/S1755-5345(13)70006-X.
Wang, Y., D’Ariano, A., Yin, J., Meng, L., Tang, T., Ning, B., 2018. Passenger demand oriented train scheduling and rolling stock circulation planning for an urban rail transit line. Transp. Res. Part B Methodol. 118, 193–227. https://doi.org/10.1016/j.trb.2018.10.006.
Xie, J., Wong, S.C., Zhan, S., Lo, S.M., Chen, A., 2020. Train schedule optimization based on schedule-based stochastic passenger assignment. Transp. Res. Part E Logist. Transp. Rev. 136 https://doi.org/10.1016/j.tre.2020.101882.
Xu, X., Liu, J., Li, H., Jiang, M., 2016. Capacity-oriented passenger flow control under uncertain demand: Algorithm development and real-world case study. Transp. Res. Part E Logist. Transp. Rev. 87, 130–148. https://doi.org/10.1016/j.tre.2016.01.004.
Yang, J., Jin, J.G., Wu, J., Jiang, X.i., 2017. Optimizing passenger flow control and bus-bridging service for commuting metro lines. Comput. Civ. Infrastruct. Eng. 32 (6), 458–473. https://doi.org/10.1111/mice:2017.32.issue-610.1111/mice:12265.
Yang, M., Liu, X., Wang, W., Li, Z., Zhao, J., 2016. Empirical analysis of a mode shift to using public bicycles to access the suburban metro: Survey of Nanjing, China. J. Urban Plan. Dev. 142 (2), 05015011. https://doi.org/10.1061/(ASCE)UP.1943-5444.0000299.
Yen, J.Y., 1971. Finding the K shortest loopless paths in a network. Manage. Sci. 17 (11), 712–716. https://doi.org/10.1287/mnsc.17.11.712.