英文题目：Simulation-Based Optimization Method for Impact Evaluation to Work Zones in Large-Scale Networks

中文题目：基于仿真优化方法的大规模交通路网施工区影响评估

论文作者：彭辰，陈荣升，姚恩建，杨扬，尚永毅

论文期刊：IET Intelligent Transport Systems

摘要：

在交通网络中，为进行道路养护而设立的施工区会显著影响交通分布和出行者的路径选择行为。本研究提出了一种方法，用于评估和预测施工区对大规模交通网络的广泛影响。为满足高效评估施工区对交通网络各种影响的需求，本研究定义了道路养护敏感度因子（Road Maintenance Sensitivity Factor, RMSF）来表征施工区的综合影响。研究构建了一个基于仿真的优化方法来标定RMSF，并构建解析性元模型来替代原始目标函数。该元模型建立了RMSF与施工区影响的交通流分布之间的近似关系。研究采用一种无求导的信赖域算法来获取最优解。在一个小型测试网络和一个大规模高速公路网络上进行了数值实验。实验结果表明，在计算资源有限的情况下，与同步扰动随机近似方法相比，本研究提出的方法在两个实验中均展现了更高的准确性和有效性，能够准确高效地给出RMSF结果，并绘制出大规模网络在有施工区时的交通再分布情况。这有助于交通管理者在交通管理系统的辅助下，优化养护计划和交通管理措施。

1. 引言

近年来，交通量的激增导致道路设施（尤其是高速公路）性能下降，道路养护变得日益重要。然而，养护施工区会通过部分关闭车道等方式降低道路通行能力，引发交通拥堵，并通过影响出行者的路径选择，将影响扩散至整个路网。准确评估这些影响对于优化养护方案至关重要，但在大规模网络中，由于影响因素多维且复杂，直接计算的成本极高。

为解决此问题，本研究提出了一个统一量化指标——道路养护敏感度因子（Road Maintenance Sensitivity Factor, RMSF），用以整合施工区对路径选择的各种影响。进而，将影响评估问题转化为一个标定RMSF值的优化问题。为了高效求解这个在高维网络中呈非凸、多局部最优解的复杂问题，本研究构建了一种基于元模型的仿真优化（simulation-based optimization, SO）方法。该方法利用交通分配模型的内在结构信息，建立一个可解析的代理模型（即元模型）来近似原始目标函数，从而大幅降低求解难度和计算成本。

2. 方法论

本研究聚焦施工区影响评估问题，该问题可转化为标定RMSF值的问题。总体思路如图1所示。基于交通管理系统收集和分析的交通量和OD（origin-destination）矩阵，施工区影响评估问题可以转化为一个RMSF标定问题，其中RMSF代表了施工区对交通流分布的综合影响。标定RMSF值后，施工区对交通流的影响就可以被量化，交通管理者可以据此进行交通管理。本节展示了标定RMSF值的方法。首先，介绍了标定RMSF值的问题。然后，提出了一种基于仿真的优化方法，并详细阐述了求解算法的结构。

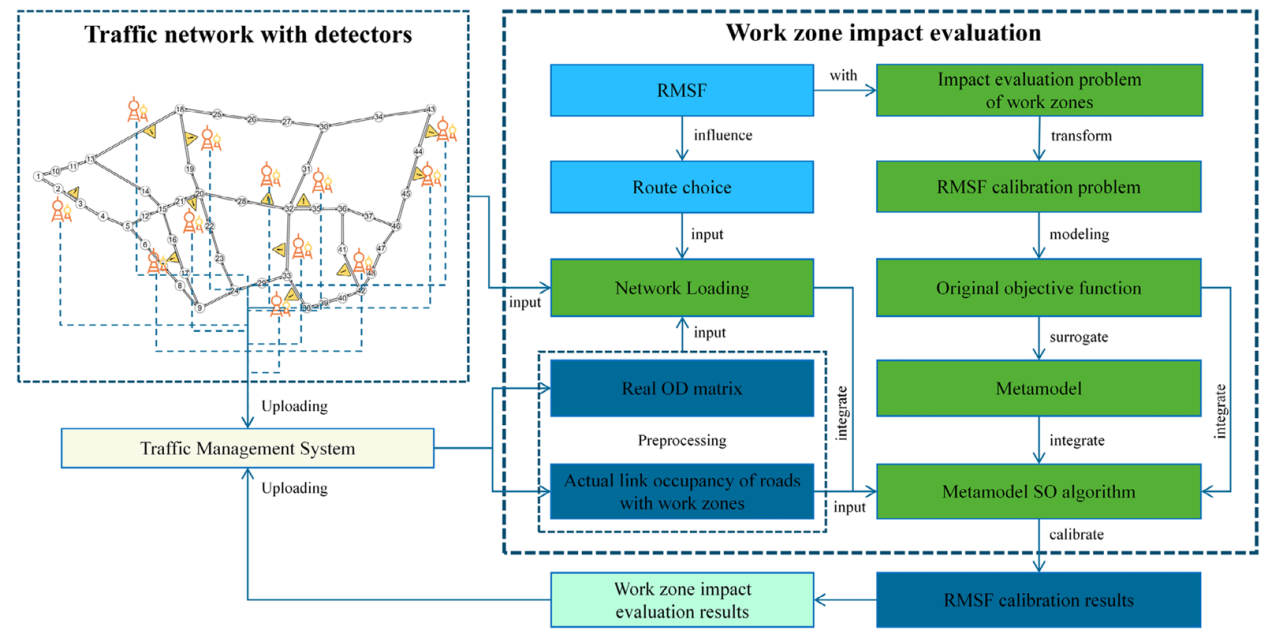
图1 施工区影响评估的总体思路

2.1 问题描述

考虑一个交通网络，其形式为有向图，包含节点集合和路段集合。根据前文讨论，本研究中的评估问题被转化为对施工区RMSF的标定问题。该标定偏差可以通过含有施工区路段上的占有量差异来反映。在这里，路段占有量指的是在给定时刻处于某一路段上的车辆数。研究中使用的符号列于表1。

标定问题的表述如下：

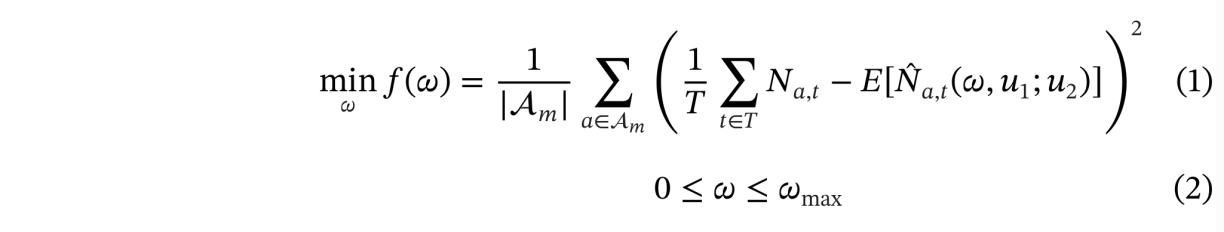
在公式(1)中，决策向量是每个路段的RMSF向量。目标函数为在指定时间间隔内，有施工区的道路上实际与仿真路段占有率之间的平均偏差。括号中的第一项表示在时间间隔T内，有施工区路段的平均实际路段占有率。第二项表示在施工区影响下，同一路段和时间间隔的仿真路段占有率的期望值。是内生变量向量（如交通需求、交通密度、出行时间），是外生参数向量（如路径选择概率系数、最大速度、施工区设置）。公式(2)定义了RMSF的取值范围。下界为零，表示道路施工区对路径选择行为没有影响。上界可以根据交通分配结果估算，代表施工区对交通状况可能造成的最大影响程度。

总的来说，这个问题旨在标定每个路段的RMSF向量。然而，解决这个问题是一个挑战。首先，由于目标函数中的仿真项是时变的、非线性的和非凸的，该问题是欠确定的，存在许多局部最优值。其次，这是一个高维问题。随着网络规模的扩大和施工区数量的增加，决策向量的维度和计算网络交通分配结果的时间都会增加。这些挑战导致了计算成本高昂的估计过程。因此，设计一种能够克服大规模网络标定挑战的高效离线标定方法至关重要，这也是本研究提出方法的目标。

表1 本研究中的符号列表

2.2 优化方法构建

2.2.1 总体框架

本研究中标定问题的优化方法是一种元模型的SO方法，根据Osorio用于使用的一般元模型SO方法来标定RMSF向量。考虑到直接用原始目标函数解决标定问题所面临的挑战以及大规模网络实践中的标定效率，需要一种能够在少量迭代中减少计算负担的方法。此外，在大规模网络中计算交通分配结果的成本很高，导致计算预算紧张，因此计算框架的短期性能也值得考虑。本研究构建了一个高效的解析模型，称为元模型，它为原始目标函数提供全局和局部的近似，可以直接求解以避免高昂的计算成本。这也使得在有限的计算预算内能够高效地探索高维可行域，并显著提高计算效率。

如图2所示的求解算法由三个部分组成：

1、元模型模块：被构建为一个带有参数向量的参数化解析函数，通过收集的观测点来近似公式(1)中所示的原始目标函数。

2、模型拟合模块：拟合元模型的参数向量。

3、网络加载模块：通过计算由元模型标定的RMSF得到的交通分布结果，来评估施工区的影响。这些结果随后被用来计算原始目标函数，并估算有施工区路段上实际与仿真路段占有率之间的偏差。

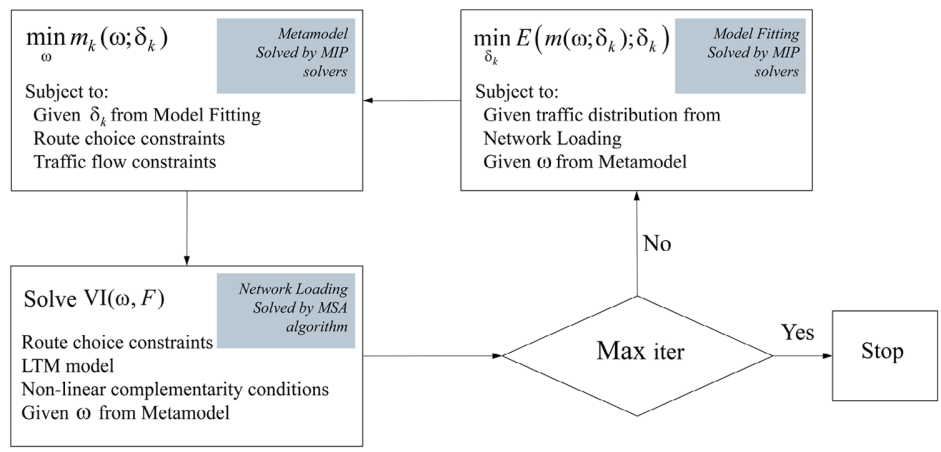
图2 所提模型的求解算法流程图

2.2.2 网络加载

为网络加载模块提出了一个随机动态交通分配模型，以表示存在施工区的动态交通流分布。该模型用于在测量或预定的交通需求下进行交通分布计算，利用内生变量和外生参数的数据。交通分布结果为每个时间步提供了每个路段上的交通量。本研究构建了基于Lo等人研究的随机动态用户均衡（stochastic dynamic user equilibrium, SDUE）模型来模拟路径选择行为和交通分布。该模型为网络加载提出了一个基于离散时间运动波的路段传输模型（link transmission model, LTM）。网络加载的目标是最小化所有出行者的总感知出行时间。该模型的约束可分为四个部分：流传播、流守恒、路径选择概率和随机动态用户均衡。对于路径选择概率约束，我们将RMSF整合到路径的效用中。

1、流传播：该模块模拟了路段的发送流、接收流与每个时间步交通流之间的关系。它根据每个时间步的交通量和路段的最大通行能力计算发送流和接收流。然后，下一时间步进入和离开路段的累计车辆数被定义为当前时间步的累计数与下一时间步相应流入/流出量之和。

2、路径流守恒：该模块建立了路径交通流与路段交通流之间的关系，它将路段流量计算为通过该路段的所有路径流量的总和。此外，该模块给出了路径流量的下界以及基于自由流速度的流入和流出之间的约束。

3、路径选择约束：

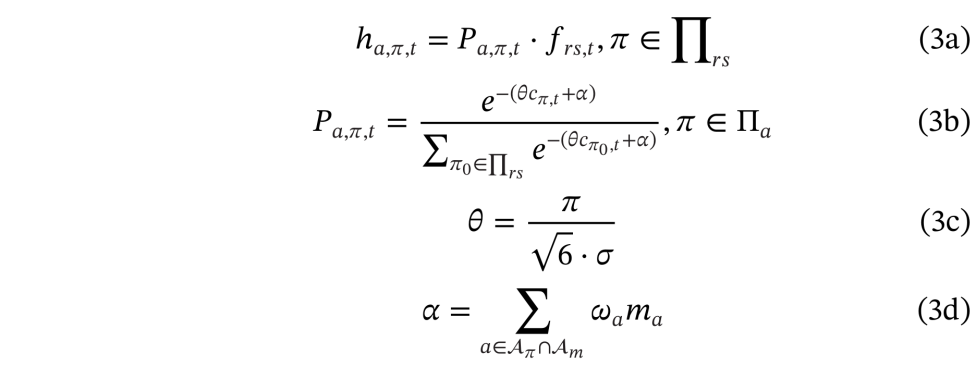
公式(3a)表明，在时间t的路径流量等于始发地和目的地之间的总需求乘以路径选择概率。公式(3b)基于每条路径的效用函数计算路径选择概率，其中包括了RMSF的影响。公式(3c)表示路径选择效用系数与感知出行时间标准差之间的关系。公式(3d)表明路径选择效用受到施工区长度和RMSF的影响。

4、随机动态用户均衡：

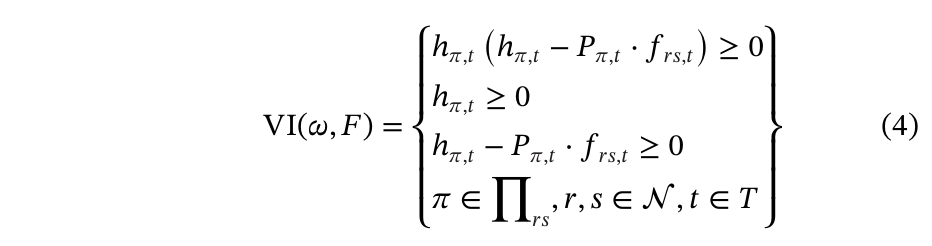
公式(4)是SDUE下的一个互补约束。对于每个时间步t，每条被选路径上的交通量是OD对(r,s)之间的总需求与路径选择概率的乘积，而每条未被选路径上的交通量为0。

2.2.3 元模型构建

元模型方法的主要思想是构建一个解析的、针对特定问题的函数，该函数带有一组非线性方程，称为元模型，通过在上述算法的每次迭代中利用交通分配模型的结构信息来近似原始目标函数。元模型旨在确定每次迭代中RMSF的最优值。在优化算法的第k次迭代中，元模型优化问题公式化如下。

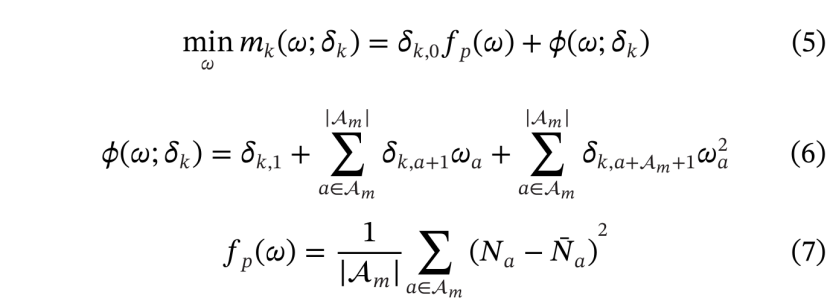
公式(5)表明元模型由解析交通模型提供，作为原始目标函数的近似，并通过缩放因子和多项式函数进行调整。多项式函数（公式(6)）是一个二次多项式，其缩放因子为，求和项的数量与决策向量的维度有关。另一方面，解析交通模型构建了公式(1)的一个针对特定问题的、解析且可微的近似形式，定义为公式(7)。一个路段在给定时间步的车辆占有率可以通过计算驶入该路段的车辆总数与驶出该路段的车辆总数之差得出，如图3所示。

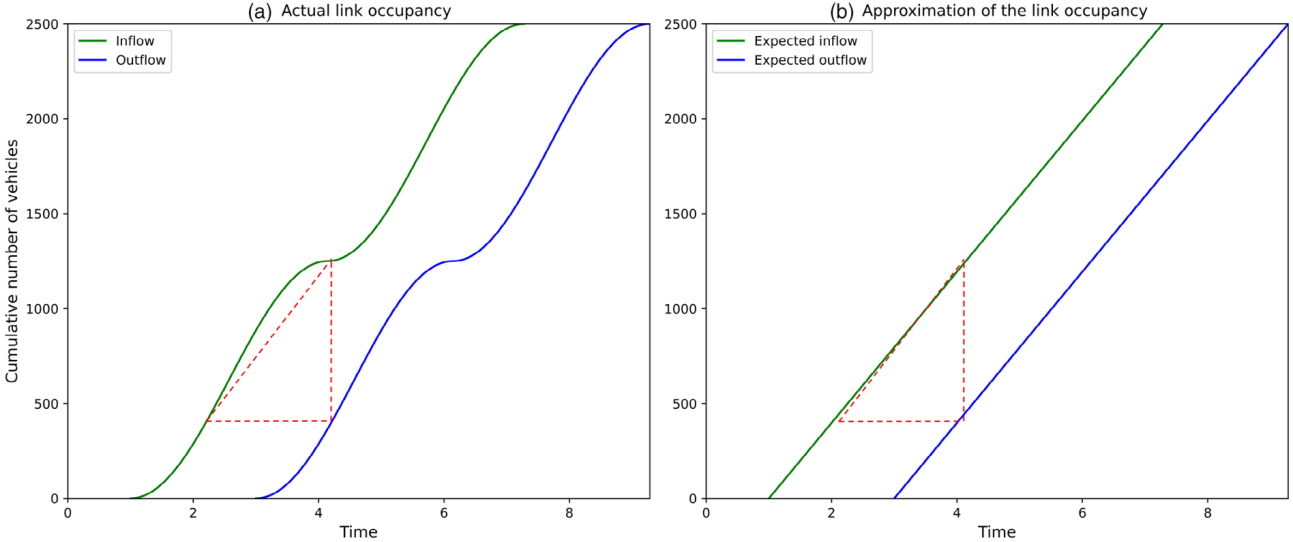
图3 路段上路段占有率的近似

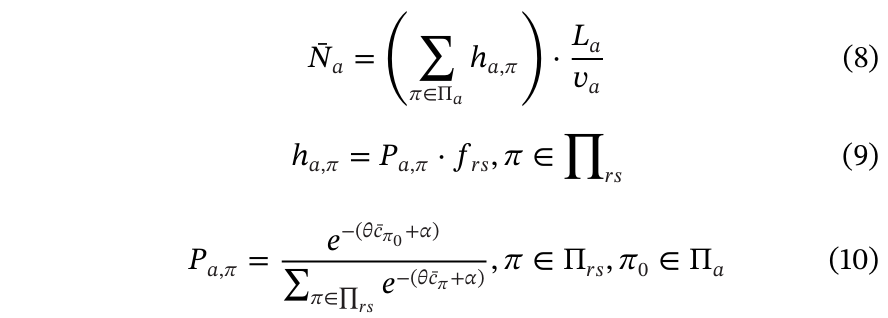
公式(8)表明路段的期望路段占有率等于进入该路段的所有路径上的期望交通量与该路段的期望出行时间的乘积。公式(9)表明路径流量等于OD对(r,s)之间的总需求与选择该路径的流量比例的乘积。与网络加载中的路径选择概率函数类似，元模型考虑了施工区对出行者在路段上路径选择行为的影响。在公式(10)中，它已被更改为不随时间变化的静态公式，以便集成到解析元模型中。

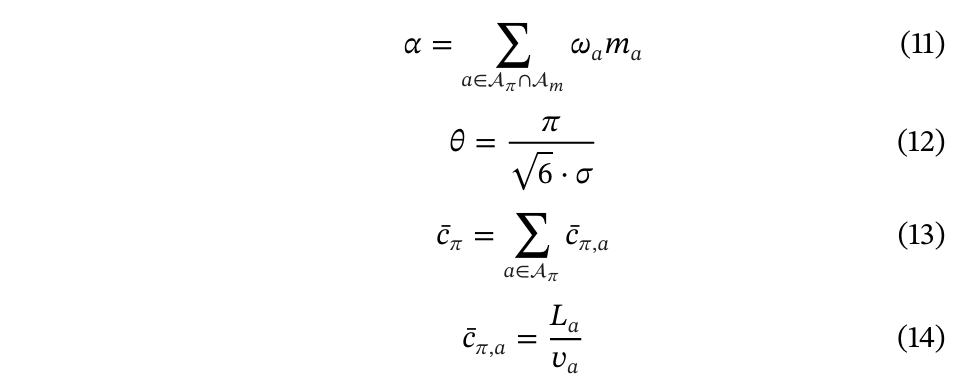
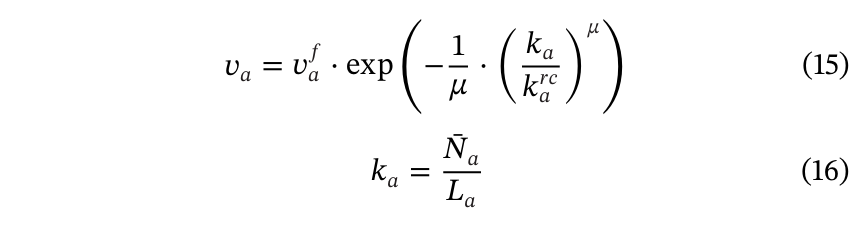
为了准确近似原始目标函数，元模型实现了交通流模型中交通流量、速度和密度关系的近似映射。

宏观交通流模型可以准确捕捉网络中交通速度和密度之间的关系，这表现为基本图。由于需要拟合现实世界条件，描述这些关系的表达式通常是非线性的，甚至是分段的非凸函数，这不能直接用作优化模型中的约束，也增加了计算难度。因此，本研究采用METANET中的速度-密度关系式（公式(15)）作为梯形基本图的近似，其中是梯形基本图的右临界密度，是一个可调整以近似LTM基本图的参数。这个公式经过测试可以很好地拟合LTM模型中的原始宏观交通流模型。而且，尽管这个公式是非线性的，但它是连续且平滑的，显著降低了优化模型获得最优解的复杂性。

2.3 求解算法

为了标定RMSF值，图2中的三个模块被整合到一个无导数信赖域框架中。令表示在第k次迭代时的元模型。所提方法的求解算法如算法1所示。

该算法避免了传统信赖域算法中求解信赖域子问题梯度的步骤。它也不同于传统的元模型方法，后者在网络加载后需要大量迭代来获得交通分配结果，带来了巨大的计算负担，尤其对于大规模网络优化。该算法有效地将交通分配过程与解析模型拟合相结合，避免了过多的额外仿真运行，这使得所提方法在大规模网络中具有优势。

所提方法的算法在次迭代中的总计算时间复杂度为：

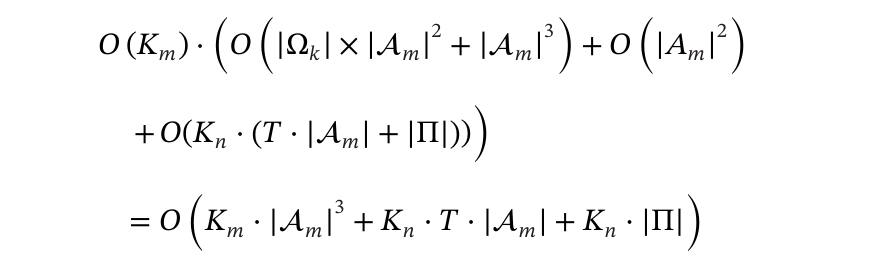
这是一个多项式时间复杂度，因为它由输入大小和的多项式函数项组成。由于不存在指数或阶乘项，整体复杂度属于多项式时间类。

算法1 元模型SO算法

3. 数值实验

3.1 性能验证

为了验证第2节中构建的优化方法的性能，构建了一个测试交通网络（见图4）来标定施工区的RMSF。该网络基于Ziliaskopoulos的研究构建，包含6个节点和7条有向路段。网络中有一个从节点1到节点6的单一OD对，有三条不同的路径。在路段(4,5)上设置了一个500米长的道路施工区。

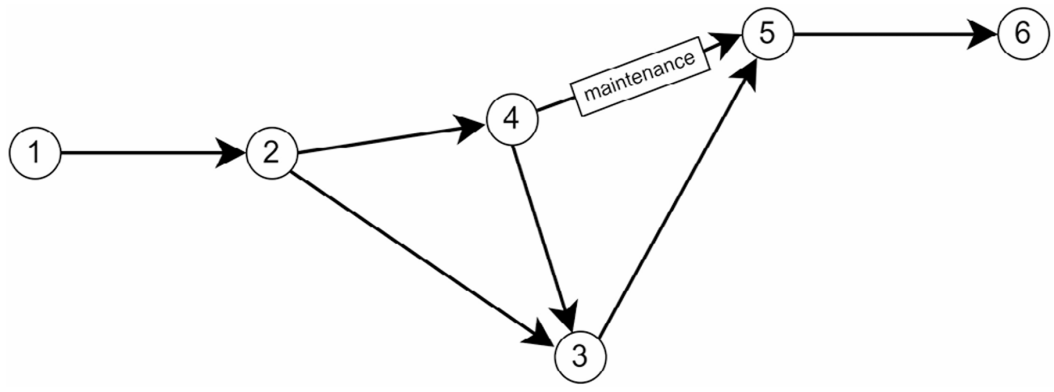
图4 用于标定方法验证的Ziliaskopoulos网络

这是一个一维标定问题，用于评估元模型的拟合和标定性能。图5展示了在不同参数值组合下，元模型的解析部分与原始目标函数在可行域内的值。结果表明，元模型的解析交通模型部分在所有测试的参数值组合下都为原始目标函数提供了准确的近似。

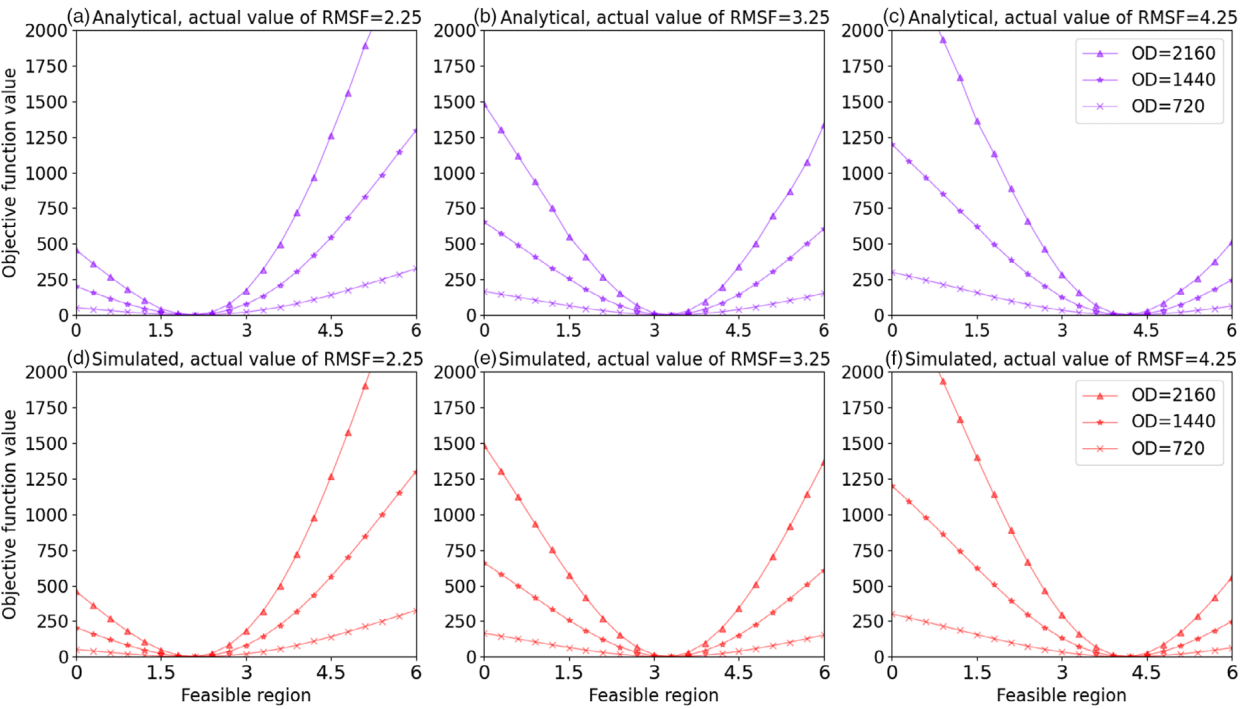
图5 元模型解析部分与原始目标函数值的比较

接下来，我们求解该网络中的RMSF标定问题，以测试所提模型的性能。我们将所提方法与作为基准方法的同步扰动随机近似（simultaneous perturbation stochastic approximation , SPSA）算法进行性能比较。选择SPSA作为基准方法的原因在于：作为一种启发式算法，它基于随机近似的逻辑，与所提方法不同。SPSA通过同时对所有变量进行随机扰动来估计梯度，这使其在处理高维优化问题时非常高效。

图6显示了元模型和SPSA方法在不同仿真运行次数下的标定结果。图5显示，在所有十次实验中，元模型在第一次仿真运行时就找到了最优的RMSF值，原始目标函数值降低到小于1，这表明即使在计算预算有限的条件下，元模型也能具有良好的标定性能。通过比较两图，可以明显看出，作为基准标定方法的SPSA性能不如所提方法。

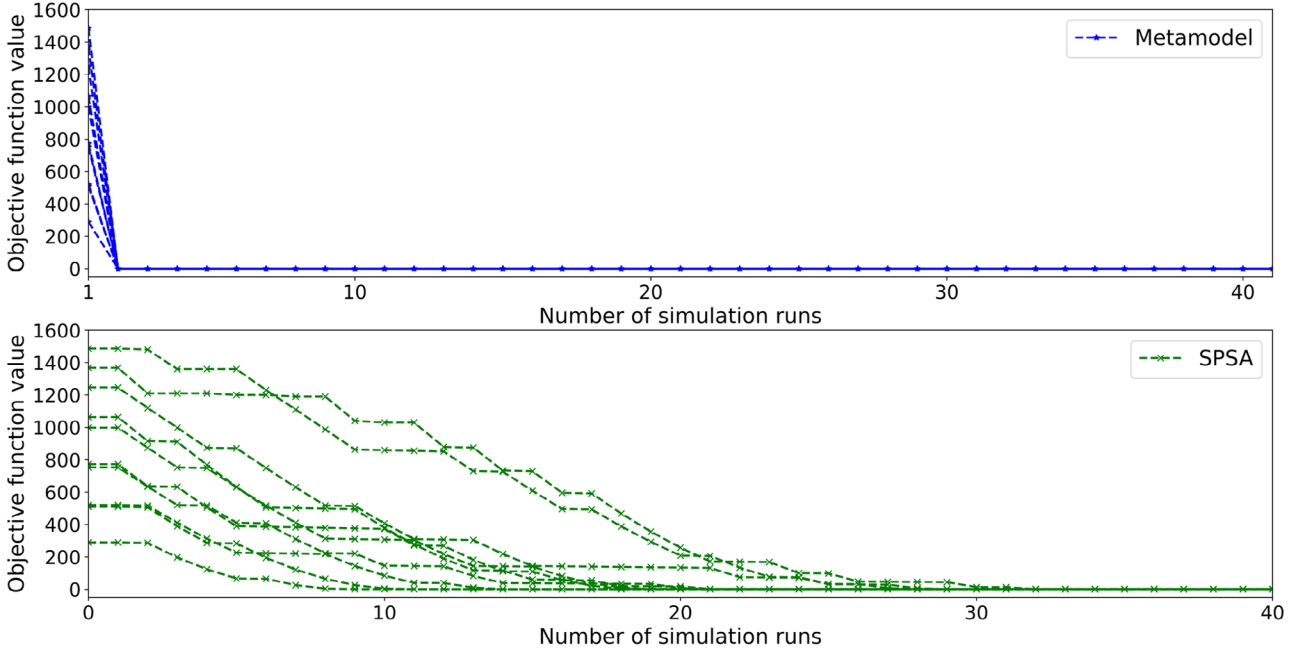
图6 元模型与SPSA方法标定结果的比较

3.2 大规模高速公路网络案例研究

为了评估所提方法在大规模网络中的性能，并进一步测试在多个路段上对施工区RMSF的标定性能，我们使用了一个位于中国广西省南宁市的扩展高速公路网络，如图7a所示。

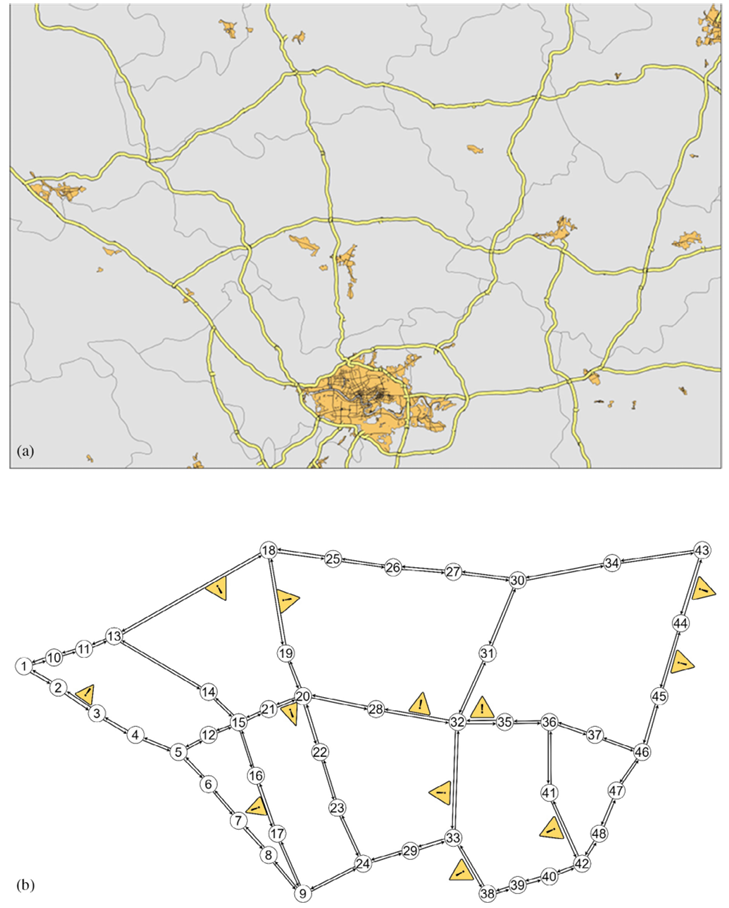
图7 (a) 广西高速公路网 (b) 仿真网络模型

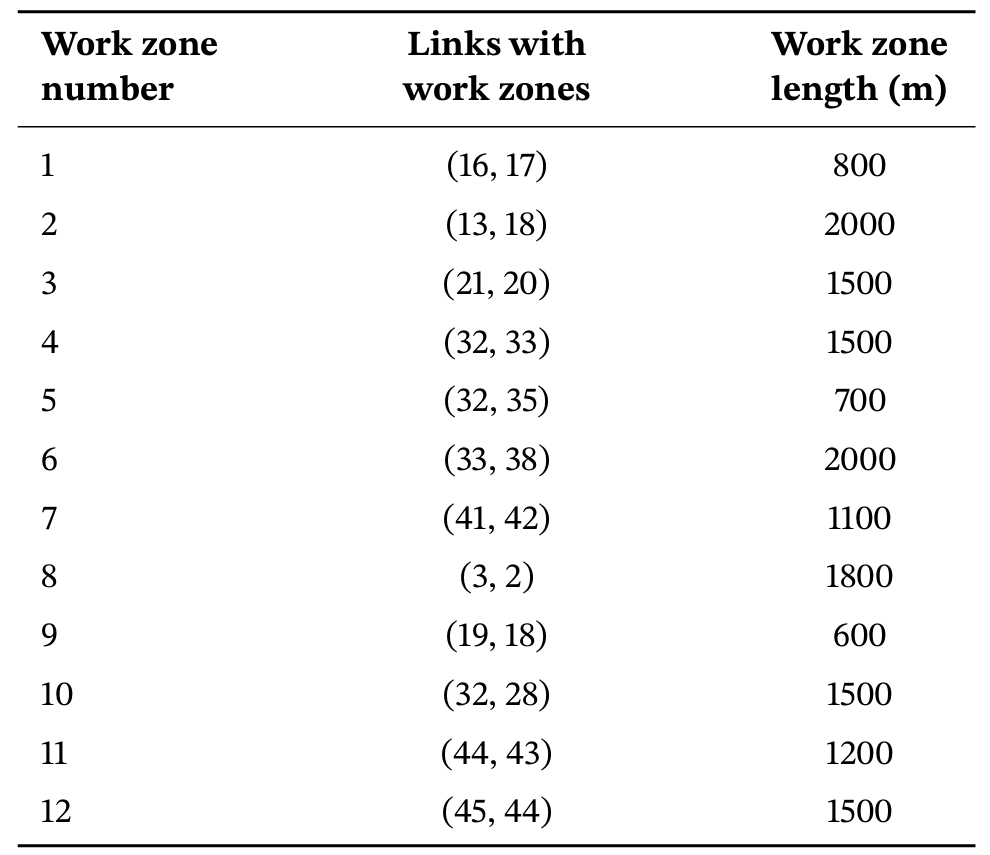
仿真网络被构建为一个包含48个节点和112条路段的有向图，如图7b所示。在网络中随机选择了12条路段，设置了不同长度的施工区（如表2所示）。

表2 高速公路网络施工区的信息

3.2.1 标定实验

本研究中的方法的标定性能评估基于两个维度：计算预算和计算时间。我们随机选择了十组参数值作为RMSF向量的初始值，然后算法迭代标定RMSF。同样，选择SPSA方法与本研究提出的方法进行比较。

图8显示了原始目标函数的结果，z轴表示有施工区路段交通量的偏差，x轴表示仿真运行次数。根据结果，所提方法在第一次迭代中就取得了优异的标定结果，两个初始采样点使得误差至少降低了两个数量级，并在几次仿真运行后进一步改善。相比之下，SPSA在拥有更多计算资源的情况下，经过20次运行后仅使目标函数降低了20%。

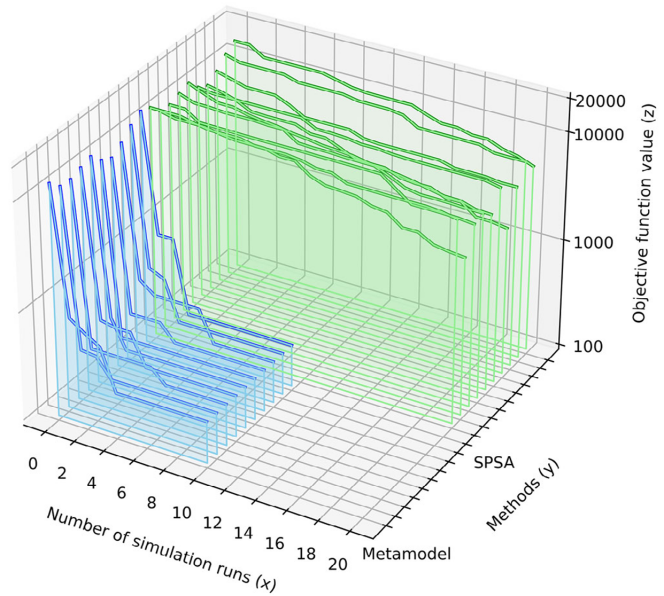
图8 元模型与SPSA方法在不同仿真运行次数下的标定结果比较

考虑到元模型和SPSA方法之间计算时间的明显差距，我们为SPSA额外增加了20次迭代进行进一步比较。即使经过40次仿真运行，SPSA方法的标定结果改善有限，与元模型算法的标定结果仍有两个数量级的差距（图9和图10）。

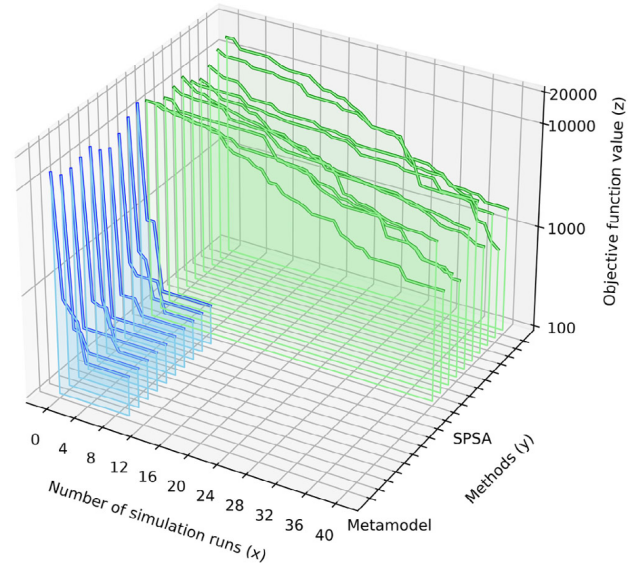
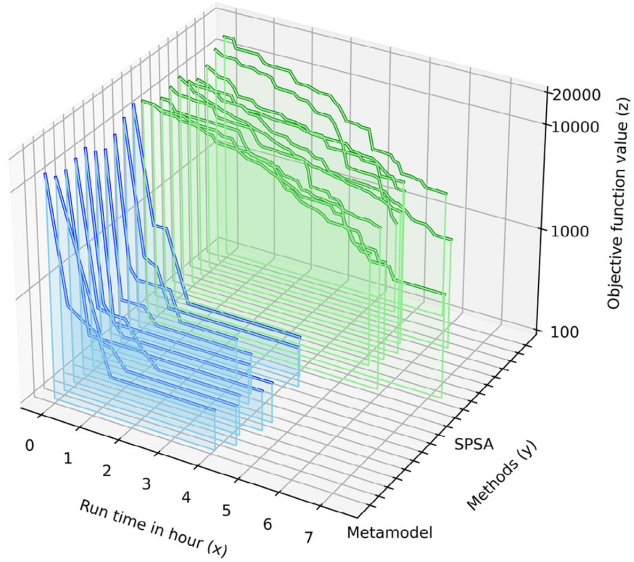
图9 仿真运行次数增加下元模型与SPSA的标定对比图10 元模型与SPSA方法的比较及运行时间

3.2.2 标定结果分析

本研究所提方法在标定带有施工区的路段的RMSF值方面已证明其高效性。图11展示了基准SPSA方法与本研究提出的方法在十次标定实验中最终标定出的RMSF结果分布的比较。本研究提出的模型表现出良好的标定性能，标定结果值与实际RMSF值非常接近。标定值与真实RMSF值的平均偏差约为15%。相比之下，SPSA方法的标定结果不太稳定，平均偏差大于30%。

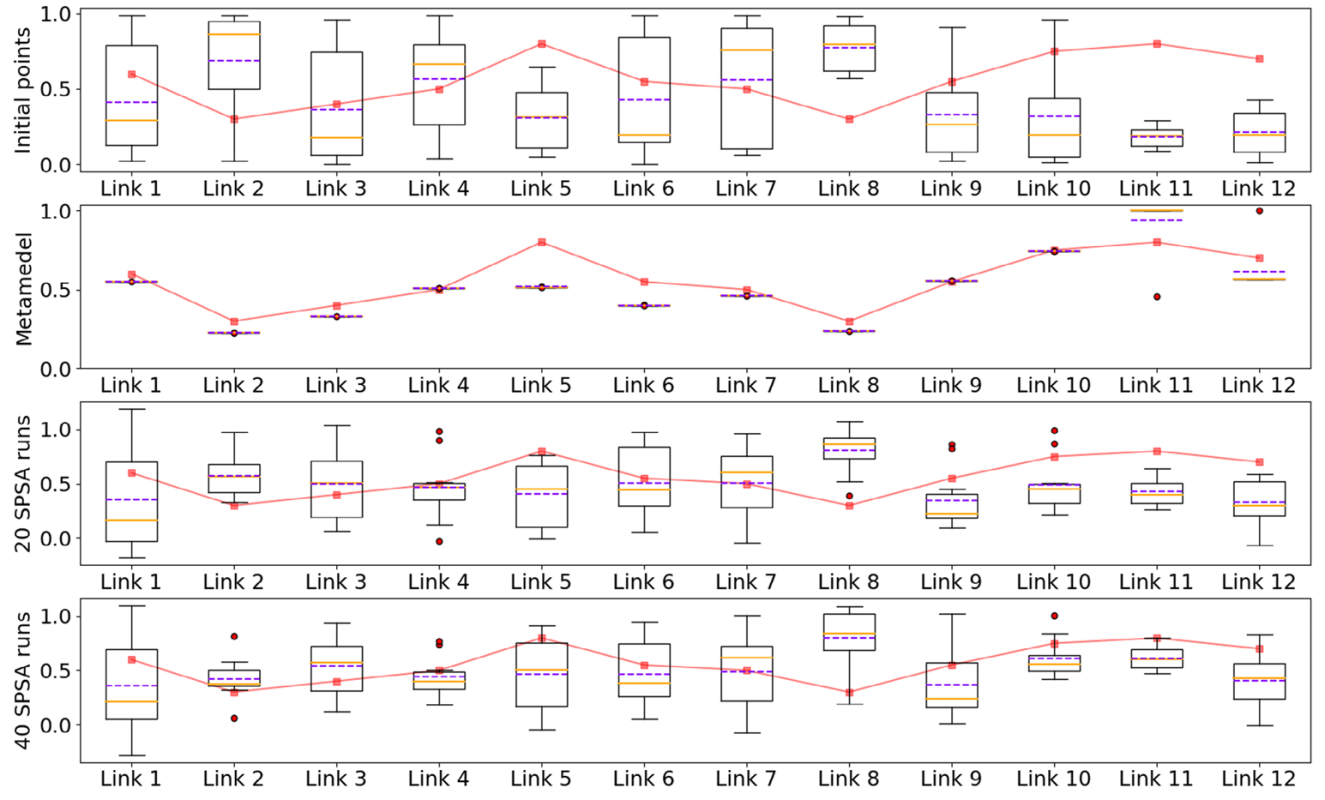
图11 元模型与SPSA方法标定结果分布的比较

图12和图13中的颜色展示了高速公路网络中每个路段的交通流分布。图表中深紫色表示高交通量，而浅黄色则表示低交通量。路段的交通量在图12和图13之间进行比较，揭示了施工区域对网络交通流分布的影响。对于大多数有施工区域的道路，施工区域的存在显著影响了旅行者的路线选择行为，RMSF值越高，旅客选择有施工区域的道路概率越低，因此路线变化行为导致大多数有施工区域的道路交通流显著减少，而邻近道路的交通流则增加。同时，某些道路的交通流量增加或甚至出现拥堵，例如（33, 32）和（32, 28），这并不是因为这些道路本身的施工区域，而是由于施工区域导致的其他道路的路线调整。这突显了施工区域，特别是多个施工区域对交通流分布的广泛影响。

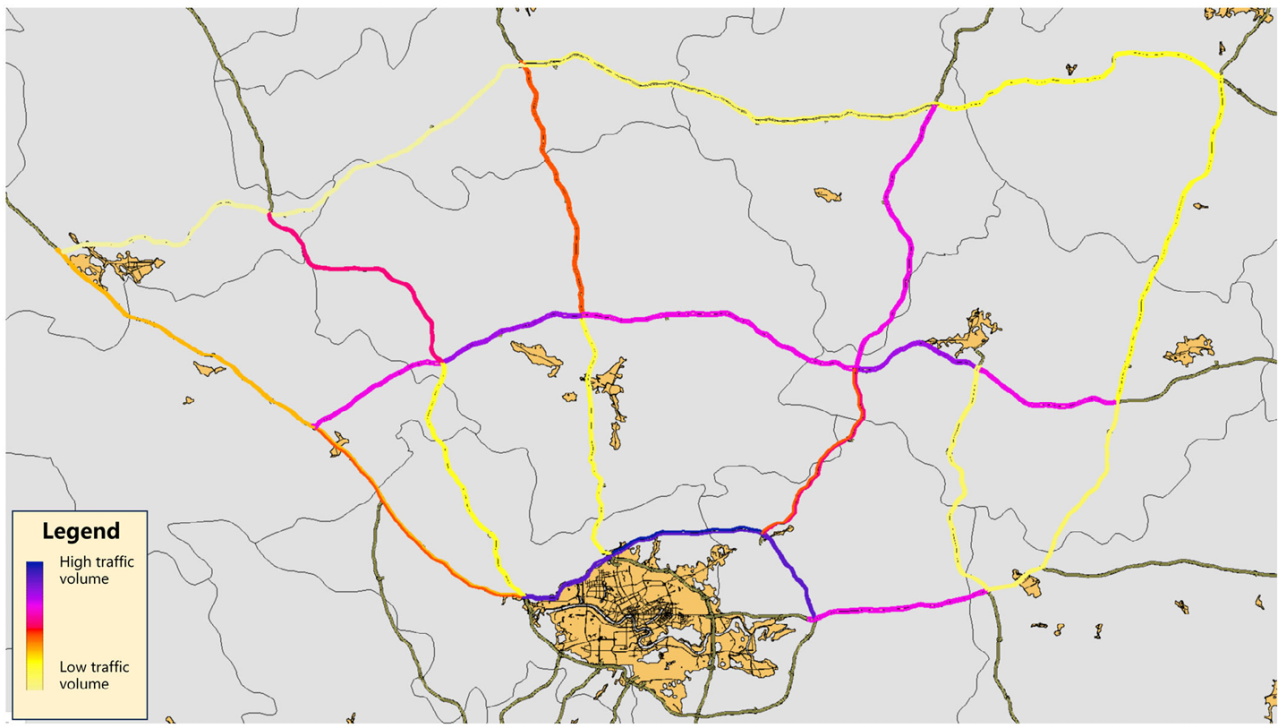
图12 无施工区时的交通流分布图

图13中道路旁边标记的数字显示了带施工区域的道路上标定交通流量与实际交通流量之间的百分比偏差。带施工区域的道路交通流量的百分比偏差在5%以内，实际道路交通流量分布在自由网络中得到了准确反映。总之，本研究中提出的方法成功地标定了RMSF，以准确高效地测量多个施工区域对大规模网络中交通流的影响。此外，结果表明，所提出的模型可以准确映射高速公路网络中的交通流分布，为交通管理者提供施工区域对网络影响的评估，协助交通管理的发展。

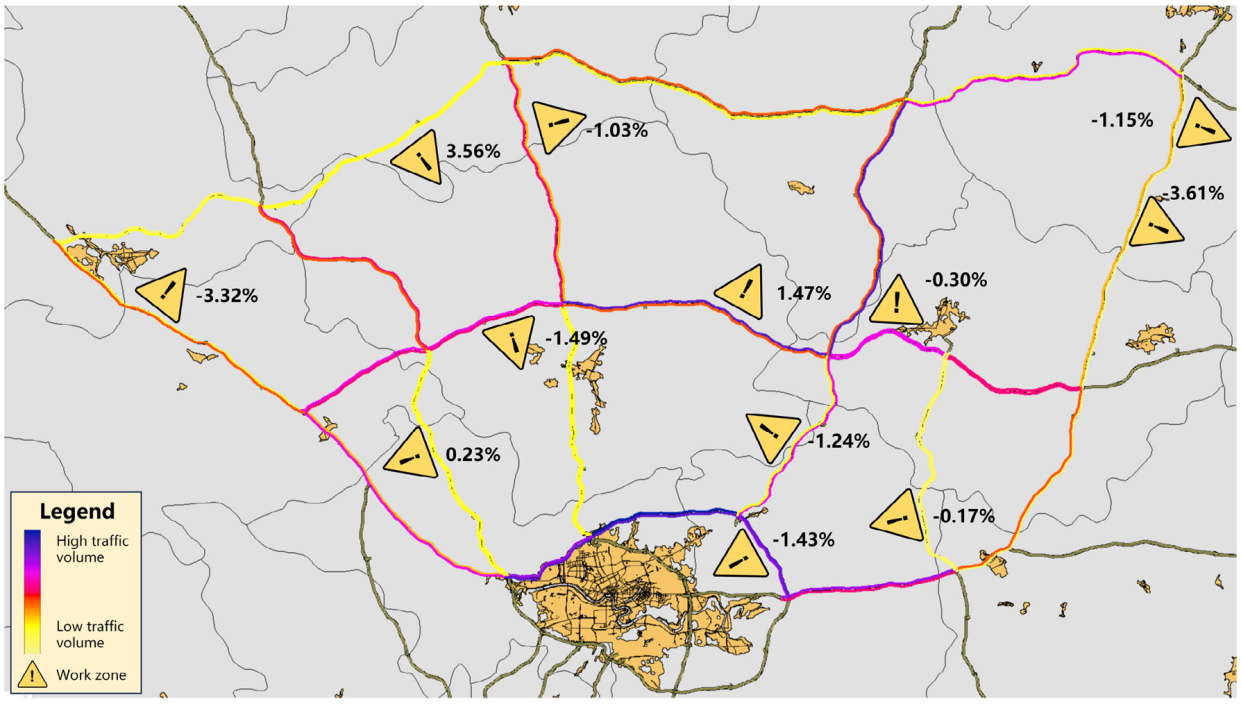
图13 有施工区时的交通流分布图及标定偏差度量

3.2.3 灵敏度分析

为展示本研究提出方法的鲁棒性和效率，本节分析了不同场景下的扩展实验。我们设置了三种不同的速度限制（108、90和80 km/h）和三种不同的交通量情景。图14显示了在不同情景下元模型和SPSA方法在计算时间上的标定效率比较。很明显，本研究提出的方法在所有九种不同情景下都远比基准SPSA方法高效。

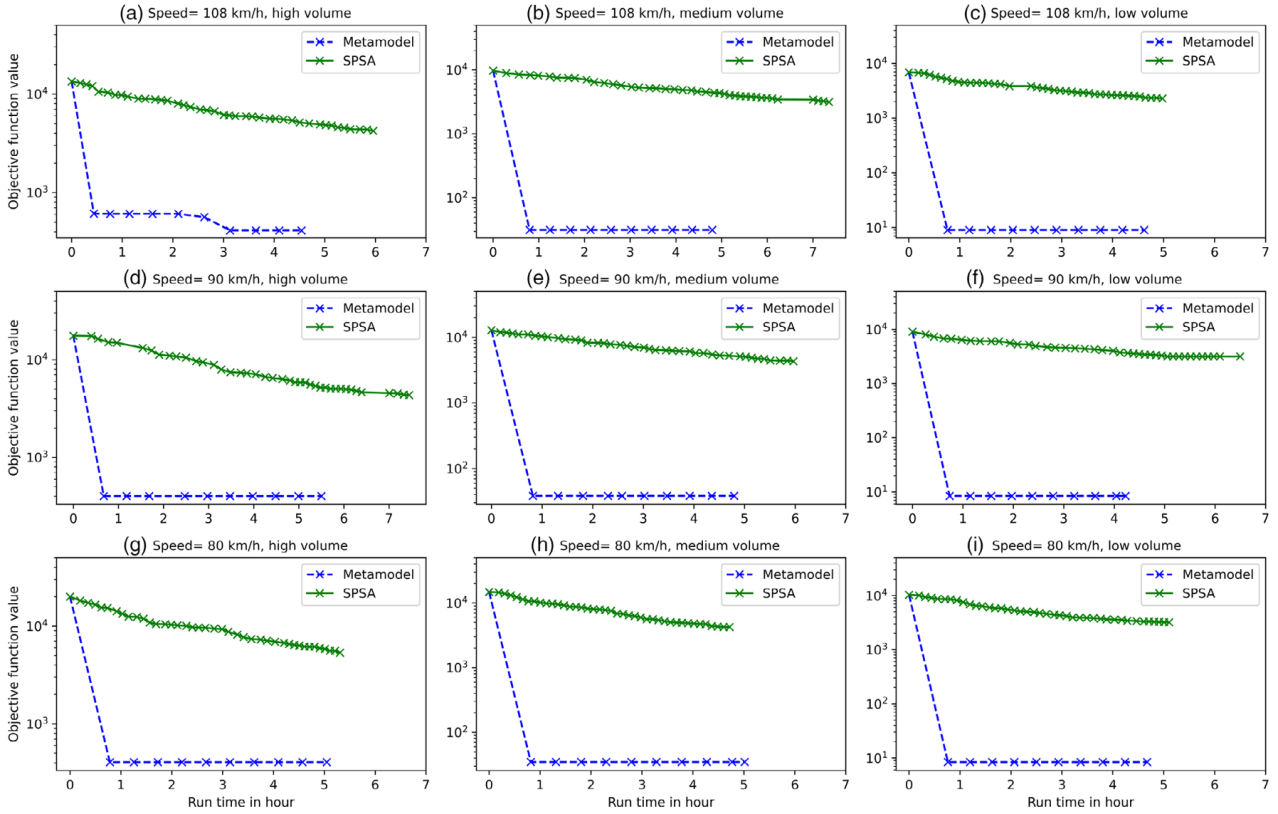
图14 不同情景下元模型与SPSA方法计算时间的比较

图15比较了所提方法与基准SPSA方法的标定结果。结果显示，蓝色条（所提方法）始终比绿色条（SPSA）短，且颜色分布更集中，表明所提方法在九个实验中的准确性和稳定性均优于SPSA方法。

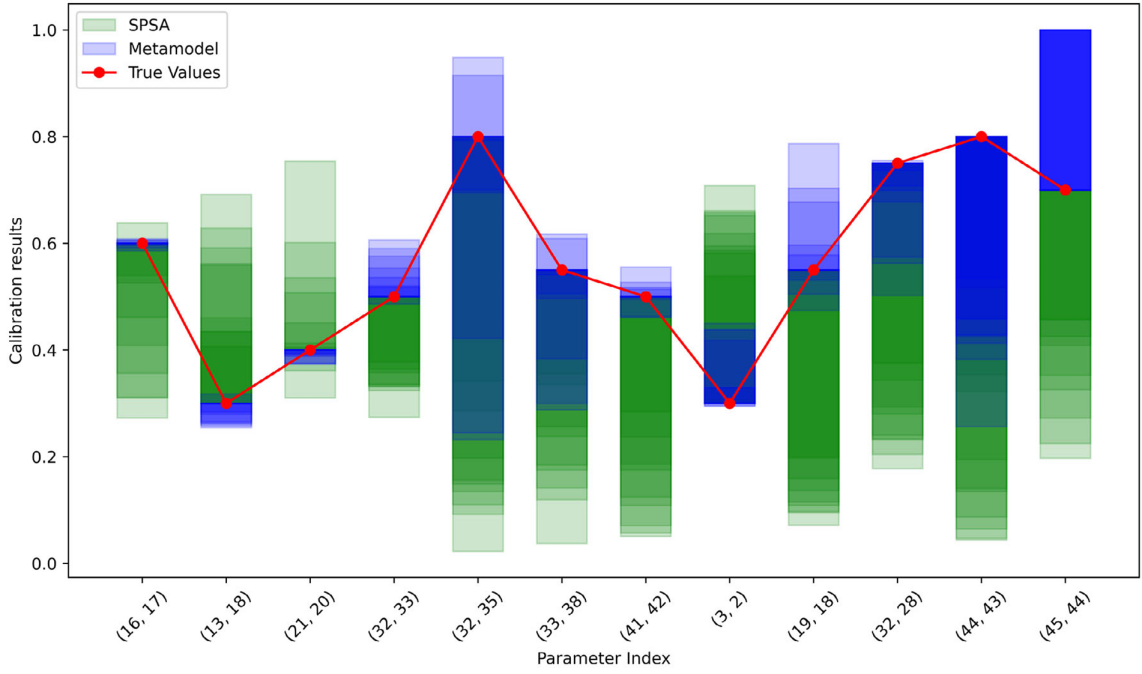
图15不同情景下元模型与SPSA方法标定结果的比较

此外，随着施工区数量的增加，本研究提出方法的计算时间呈线性增长。在所有四种施工区数量设置中，所提方法的标定效率显著优于基准SPSA方法（图16）

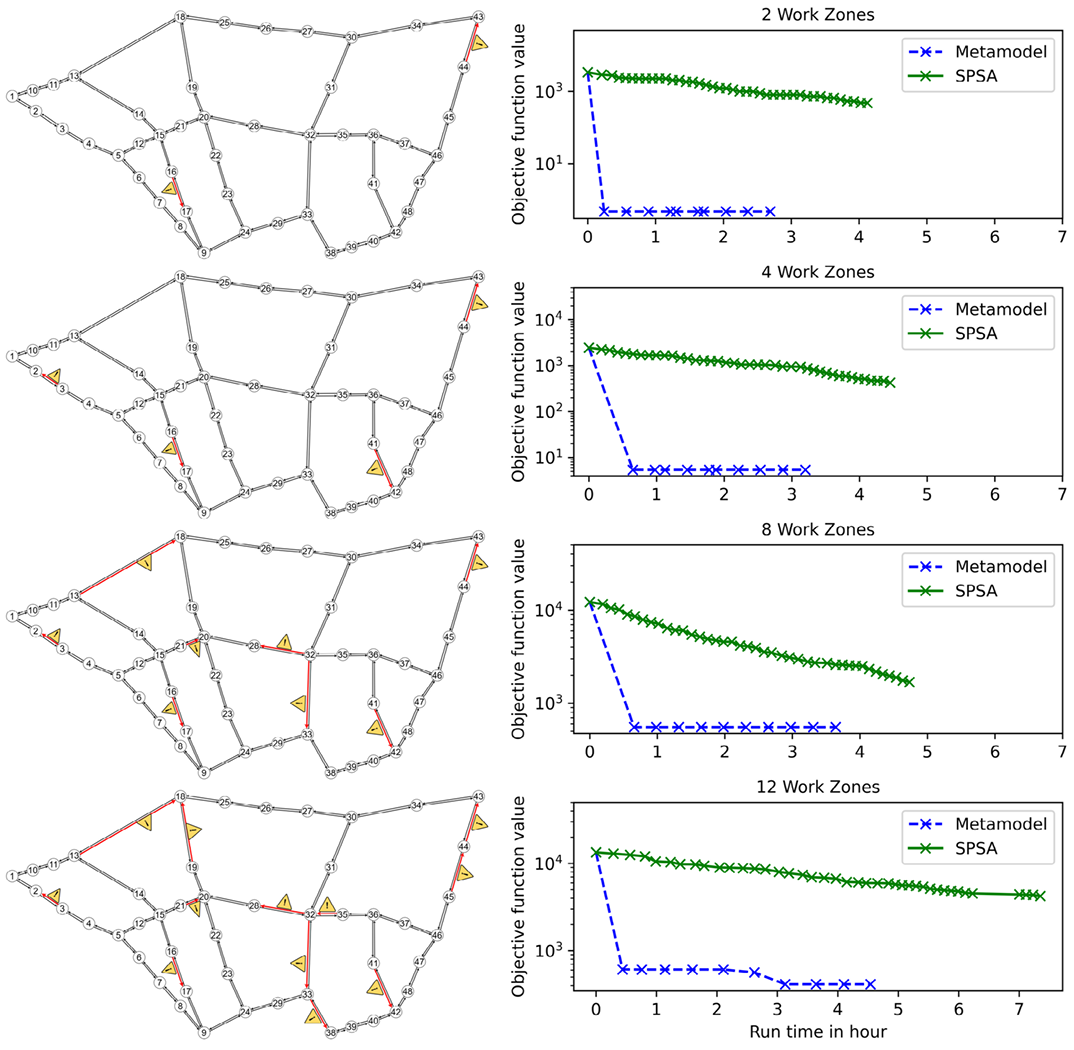
图16 不同施工区数量设置下元模型与SPSA方法计算时间的比较

4. 讨论

本研究所提出基于仿真的优化方法在大规模交通网络施工区影响评估中的表现表明，使用元模型能够在显著降低计算成本的同时，保持结果的精度和可靠性。通过与传统SPSA方法的对比实验可以看出，该方法在标定RMSF时收敛更快，且对大规模网络具有更好的适用性。这意味着在实际的交通管理场景下，管理者可以利用该方法高效地估计施工区对交通流分布的整体影响。

此外，本研究方法在捕捉施工区多因素综合作用时的优势尤为明显。RMSF的引入使得原本复杂的交通扰动能够通过一个统一的指标加以量化，从而为交通管理提供简洁、可操作的评估工具。与此同时，该研究也承认在动态交通环境下，元模型仍存在一定的近似误差。未来的研究应进一步结合更精细的交通流模型以及实时交通数据，以提升预测能力和适应性。

5. 结论

本研究提出了一种基于仿真的优化方法，用于评估大规模交通路网施工区的交通影响。研究通过引入RMSF，将施工区的综合效应转化为可标定的参数，并采用元模型替代原始目标函数，从而在保证结果精度的同时显著降低了计算复杂度。

数值实验结果表明，该方法在小型测试网络和大规模高速公路网络中均表现出较快的收敛速度和较高的标定精度，并在计算效率方面明显优于传统的SPSA方法。这一结果说明，元模型优化框架能够在有限算力条件下，为施工区影响的定量化评估提供可靠支持。

本研究的贡献主要体现在三个方面：一是提出了结合仿真与元模型的优化方法，使复杂的施工区影响评估问题能够在大规模网络中高效求解；二是通过对RMSF的标定，为交通管理者提供了量化施工区影响的实用工具，有助于施工计划和交通管理策略的优化；三是方法具备较强的拓展性，可与智能交通管理系统结合，并在未来进一步应用于多施工区情境和动态交通数据环境。

未来的研究方向包括两点：其一是结合实时交通数据，以提升RMSF的动态标定能力；其二是探索方法在更复杂的交通网络结构以及多施工区并发条件下的适用性，从而进一步增强其在实际交通管理中的应用价值。