Multistage charging facility planning on the expressway coordinated with the power structure transformation

英文题目:Multistage charging facility planning on the expressway coordinated with the power structure transformation
中文题目:与电力结构转型协调的高速公路多阶段充电设施规划
论文作者:张天雨,姚恩建*,杨扬,Hong-Ming Yang,郭东博,David Z. W. Wang
论文期刊:Computer-Aided Civil And Infrastructure Engineering
论文网址:https://doi.org/10.1111/mice.13216
摘要:
本研究提出了一个新型的高速公路快速充电站(Expressway Fast Charging Station, EFCS)多阶段规划问题,该规划与区域 电力结构(Power Structure, PS)的动态转型相协调。在 EFCS 网络可持续运营、网络可达性和有序建设的前提下,开发了一种面向节能减排(Energy Saving and Emission Reduction, ESER)、效益提升和设施利用合理化的三步规划方法: (i)电动汽车扩展网络, (ii)基于多智能体的动态交通分配(MA-DTA)以及(iii)部署优化。将 MA-DTA 和定制优化策略嵌入到迭代规划结构中,实现了 EFCS 网络的运营与规划一体化。在山东半岛城市群进行了数值实验和实证研究。结果表明,该方法可以在可接受的计算时间内找到高质量的解,并适用于现实中的大规模高速公路快速充电站规划。该规划法能有效利用经济与设施引导电动汽车用户充电需求,提升整体 ESER 效益,且运营规划一体化在全时段合理匹配设施服务与充电负荷供需上效果显著。此外,探讨了 2025-2045 年期间的多阶段EFCS 规划方案,并揭示了一些有见地的政策启示。
关键词:电动汽车;充电行为;路径选择行为;混合选择模型;规划能力
1.引言
目前,在交通运输节能减排政策和社会认可度提升的推动下,电动汽车(EV)市场呈现出强劲的发展势头,政府越来越重视 在高速公路上建设充电网络(IEA,2023)。截至 2022 年 10 月,中国 6618 个高速公路服务区中的 3974 个已建成 16,721 个充电站。然而,现有网络无法有效满足电动汽车用户中长途出行的增长需求,因为设施供需不匹配的问题仍然突出(Kang 等,2022)。作 为能源补充基础设施,合理部署高速公路快速充电站(EFCS)网络是保障电动汽车城际出行、确保运营商盈利能力以及实现高速公路ESER 目标的重要基础。
为了促进 EFCS 网络建设,政府期望通过能源结构转型(Bogdanov 等,2021)来实现发电(PG)的脱碳。电动汽车(EVs)可以清洁运输的终端能源使用,但其电力来源备受批评。大多数充电站的电力来自火力发电(TP)厂(Rietmann 等,2020)。在当前的中国电力结构(Power structure, PS)中,电动汽车的整个生命周期每 100 km CO2 排放量为 19.01 kg ,与汽油车(GVs;Wang, Wang等,2021)相比减少了 44.1% 。为了实现真正的“零排放”,政府制定了一系列转型路径,以持续减少化石能源的比例,逐步推广绿色电力(Green Power, GP)发电。然而,受自然资源和社会经济的影响,在一个大型网络中,不同地区和不同时间的 PS 差异是不可避免的。
此外,成熟的 EFCS 网络对于未来容纳更多的电动汽车城际旅行至关重要,但它不是一次性建成的。EFCS 的部署需要动态适应不断增长的市场需求和变化的外部环境(Xie & Lin,2021)。其中,市场需求取决于车辆拥有量、电动汽车比例和电池退化程度;外部环境指的是 PS。通过在不同阶段有序建设和扩展充电设施,充电网络可以提供高服务水平(Level of Service, LOS)的充电服务,同时避免设施资源的浪费。
总之,多阶段 EFCS 规划应在空间和时间维度上平衡设施服务和充电负荷。在空间维度上,充电网络的供应和诱导需要得到充分重视。首先是为电动汽车在旅行期间提供方便和高 LOS 的能量补充。其次是通过设施部署引导电动汽车用户在区域 PS不均衡的情况下做出充电选择。在时间维度上,考虑充电需求和 PS 的动态演变,以实现有序的 EFCS 规划。文献综述将阐述当前的理论差距和本研究的动机。
1.1.1 部署方法
近几十年来,关于充电设施部署(Charging Facility Deployment, CFD)的研究非常丰富。部署方法可以分为两类:优化方法和规划方法。
大多数研究采用优化方法。根据模型结构,可以分为单层和双层优化模型。对于单层优化模型,充电需求通常集中为基于节点的需求,这是根据电动汽车用户的续航焦虑(Hu et al., 2019)、车辆轨迹数据(Yang et al., 2017)或运营数据(Zeng et al., 2019)估算的。这些模型的局限性如下:(1)忽略了车辆在交通网络上的行驶过程,难以捕捉途中的充电需求(Zhang, Yao, et al., 2023); (2)忽略了站点的排队效应。设施的容量大多简单地通过静态的停留或充电次数来估算(Wang et al., 2019)。在双层优化模型中,上层确定最优的 CFD,下层是交通分配模型,以捕捉基于流量的需求(He et al., 2018; Zhang et al., 2018)。该模型的缺点如下:(1)交通分配模型侧重于交通网络上的流量传输(Ghosh-Dastidar & Adeli, 2006; Zhang et al., 2022)。它们不适用于捕捉电动汽车的途中充电需求和模拟充电站运营。(2)动态交通分配会导致双层模型在计算上难以处理,其求解精度和计算速度难以应用于实际的大规模网络。
近年来,优化和 MCDM 方法的局限性得到了更广泛的认可。一些研究人员采用基于迭代的规划方法来解决 CFD 问题。 Morro-Mello 等人(2019)提出了一种新方法,该方法考虑了多个实体的标准,并模拟了电动汽车的充电状态(SOC)和全天的流量。为了在满足连接性和覆盖约束的同时最小化 CFD 的规模,Huang 和 Savkin(2020)提出了一种两阶段方法。考虑到电池退化、车 辆异质性和三个优化目标,Wang, Zhao 等人(2021)采用迭代优化策略规划了 CFD。基于迭代的规划方法保留了优化模型寻找最优解的概念,同时结合了规划模型的全面性和高求解效率的优势。
动机 1:受限于优化和 MCDM 方法的局限性,需要提出一种结合求解精度和实际实施的 CFD 规划方法。此外,大多数关于CFD 问题的研究将运营与规划分开。这导致EFCS 在获得的方案中难以提供可持续的服务水平(Zhao et al., 2021)。
1.1.2 规划目标
在 CFD 规划中,主要考虑了不同实体的利益,如设施运营商、电动汽车用户和电力部门。作为充电设施建设和运营的主 体,运营商关注项目的经济性。具体而言,目标函数包括投资成本的最小化、运营利润、设施服务覆盖范围和捕获的交通流量。对于电动汽车用户,CFD 需要保证其出行的便利性和经济性,并尽量减少充电事件对其出行的影响。这主要被表述为最小化出 行成本(Bao & Xie, 2021; An et al., 2020),包括充电成本、排队时间、绕行时间和出行时间。此外,一些研究人员关注交通网络与电力系统的整合。需要保证配电网络的投资经济性、供电可靠性和电能质量。目标函数主要包括基础设施投资成本的最小化、电力损耗、电压偏差和电力扩展成本。
动机 2:ESER 效益在CFD 规划中主要用作统计指标而非决策指标。ESER 效益的最大化是政府的重要驱动力之一。
1.1.3 多阶段规划
多阶段规划已应用于各种设施规划问题,并根据模型结构分为两大类。
第一类是整体规划,其中多阶段部署同时优化以获得全局最优解。然而,受模型结构的限制,这类模型考虑的因素有限,难以应用于现实的大规模规划场景。
为了解决这个问题,一些研究人员采用分阶段规划,其中每个阶段的网络部署依次进行。规划方向包括正向(Li et al., 2022)和反向(Staricco et al., 2020; Zhang, Wang, et al., 2023)。在正向规划中,网络从近阶段到未来阶段依次规划,早期阶段建设的设施被迫在未来阶段使用。在反向规划中,网络从未来阶段到近阶段依次规划。未来阶段获得的站点建设集作为近阶段规划的站点备选集输入。比较正向和反向规划,Yang et al. (2023) 发现早期阶段建设的设施可能与最终部署相矛盾,导致正向规划中设施资源的浪费或低效。从长远来看,反向规划方法获得的网络部署更为经济高效。
动机 3:上述研究为解决现实场景中的多阶段 CFD 问题提供了重要基础。在不同阶段对外部环境变化的把握需要更加全面。
1.2 目标与贡献
本研究旨在实现动态区域 PS 转型中 EFCS 的多阶段有序规划。以提高 ESER 效益为导向,提出了一种三步规划方法用于 EFCS 多阶段部署。该方法包括 EV 扩展网络、基于多智能体的动态交通分配(MA-DTA)和部署优化。选择山东半岛城市群的高速公路作为实证案例。主要贡献如下。
新问题与新模型:本研究尝试规划与动态区域 PS 转型协调的多阶段 EFCS 网络部署。规划以最大化电动车辆数量和 PS 转型带来的 ESER 效益为导向。该模型基于 ESER 设计理念、可持续运营、网络可达性和有序建设提出。因此,其模型结构新颖且复杂。
集成运营与规划的迭代规划方法:通过迭代规划结构,开发了一种三步规划方法来解决大规模场景中的多阶段 EFCS 网络部署问题。通过将改进的 MA-DTA 和定制优化策略嵌入迭代规划结构,三步规划方法实现了 EFCS 网络运营与规划的集成。数值实验和实证研究的结果表明,该方法能够在可接受的计算时间内高效获得高质量解决方案,并适用于现实中的大规模 EFCS 规划。
2. 问题描述
对于所提出的EFCS 多阶段部署问题,本研究在空间和时间维度上平衡了设施的服务和充电负荷。
2.1 空间维度
在空间层面上,EFCS 网络的能源供应和需求诱导作用需要得到充分关注。
2.1.1 能源供应
准确捕捉电动汽车用户的多重途中充电需求是EFCS 网络可持续能源供应的基础。
由于续航里程的限制,电动汽车用户在城际旅行中不可避免地需要多次充电。图 1 描绘了具有多个途中充电需求的电动汽车的抽象驾驶过程。考虑到电池退化、快速充电模式、电动汽车用户的二次出行需求和续航里程焦虑,设置了四个 SOC 阈值Sok , S exp , S1 和 S 2 ,Sok其中表示阶段 k 中电动汽车组的完全充电 SOC。随着电动汽车市场的发展,电动汽车组中二手电池的比例将逐渐增加,直到趋于稳定范围内。在本研究中,采用抽样方法来描述电动汽车组在不同阶段的电池退化情况。假设阶段 k中的有效电池容量遵循截断正态分布(Wang, Zhao 等,2021), Sok ∼Nor(μk,σk2,a,b) ,其中 μk 和σk2,是电池有效容量的均值和标准差,a 和 b 是上下限。S exp 是电动汽车途中充电的预期 SOC。快速充电桩以恒流/恒压模式运行(Murnane & Ghazel,2017)。当 SOC 较低时,快速充电桩以恒流模式运行,SOC 在 30 min 内从 20%Sok 增加到 80%Sok。如果继续充电,充电桩切换到恒压模式,大约需要 1.5 h 才能充满电。因此,考虑到充电时间的经济性, Sexp 设置为当前有效电池容量的 80%。S1 是电动汽车离开高速公路时的最小SOC,这保证了城市内旅行的后续能源需求。S 2 是电动汽车用户在驾驶时的SOC 容忍极限。
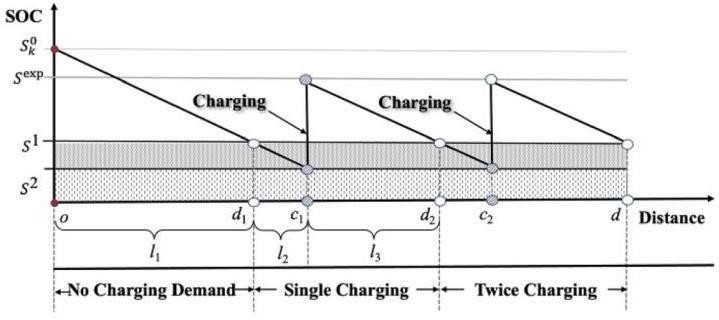
图 1 具有多个途中充电需求的电动汽车
2.1.2 需求诱导
在 PS 分布不均的地区,规划者应引导电动汽车用户前 GP 丰富的地区进行能源补充,从而提高网络的 ESER 效益。图 2 描绘了差异化充电价格和设施分配的需求诱导作用。
图 2a 是来自(o, d)的电动汽车的抽象路径。它经过一个收费站 d1 和两个充电站 c1 和 c2 ,其中电力分别来自 GP 和 TP。假 设选择路径 {o, d1, c1,c2,d} 的电动汽车需要在c1 和c2 中的任一站点充电,并且只需充电一次即可完成行程。在图 2b 中,C1 轴和 C2 轴分别表示 c1 和 c2 的广义充电成本。成本包括能源补充成本和等待时间成本。 N 轴表示同时在c1 和c2 充电的电动汽车数量。 C1min 和 C2min 表示 c1 和 c2 的最小广义充电成本,仅包括能源补充成本。假设电动汽车在 c1 和 c2 充电量相同,并且 GP 的电价设定低于TP,则 C1min < C2min。
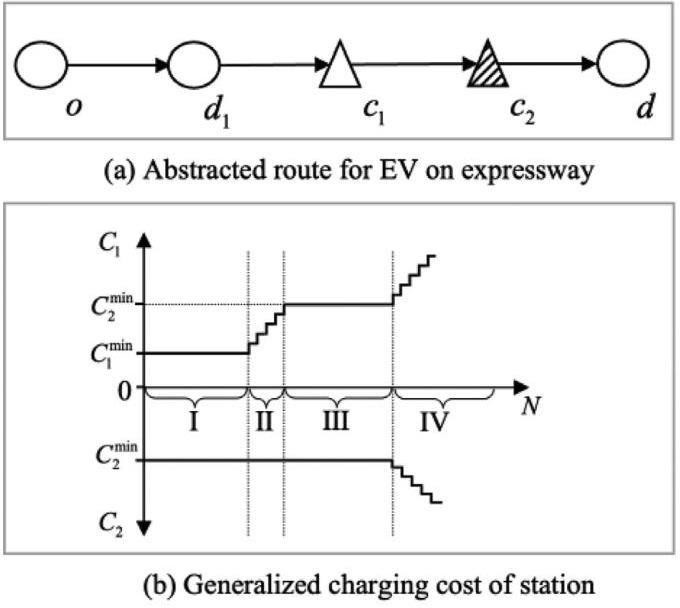
图 2 抽象充电需求诱导
观察 C1 和 C2 的增长曲线,可以将其分为四个阶段。在第一阶段,充电桩在 c1 可用,其等待时间为 0。此时,电动汽车用 户在c1 充电。在第二阶段,c1 产生排队,C1 逐渐增加但仍小于C min ,电动汽车用户仍在 c1 充电。在第三阶段,当 C1= C min 时,电动汽车用户选择c2 。在第四阶段,c1 和 c2 产生排队,电动汽车用户在 c1 和c2 交替充电。
图 2 展示了如何引导电动汽车用户在 GP 区域充电,即延长第一阶段和第二阶段的长度。第一种方法是经济诱导。通过扩大 C min 和 C min 之间的差距来增加第二阶段的长度。第二种方法是设施诱导。通过调整 c1 和 c2 中设施资源的分配来增加第一阶段的长度。所提出的模型基于上述两种方法设计。
2.2 时间维度
在多阶段EFCS 部署中,考虑各个阶段的场景变化至关重要。
随着时间的推移,除了车辆拥有量、电动汽车比例和 PS 的变化外,由于老旧电动汽车数量的增加,电动汽车群体的电池退化也不容忽视。电动汽车的电池退化主要由日历老化和循环老化引起。日历老化指的是电池随时间推移的固有退化。循环老化指的是电池在失效前可以进行的最大充放电循环次数。随着时间的推移,电池容量会有不同程度的退化。特别是对于城际旅行的电动汽车用户,可用电池容量显著影响他们的充电频率、充电量、充电地点和旅行路线。
3. 优化模型
本节提出了一个优化模型,以展示多阶段 EFCS 部署问题的数学公式。讨论了将优化模型应用于解决现实大规模 EFCS 部署的计算困难。这有助于更好地理解第 4 节中提出的方法。
3.1 优化模型
本研究从投资者、电动汽车用户和政府的角度考虑了 EFCS 的性能。对于投资者来说,建设经济性和可持续运营是关键因素。对于电动汽车用户来说,他们关注的是出行和补充能源的成本。政府需要保证 EFCS 网络的网络可达性,并关心其 ESER效益。考虑到上述因素,提出了一个广义优化模型如下。
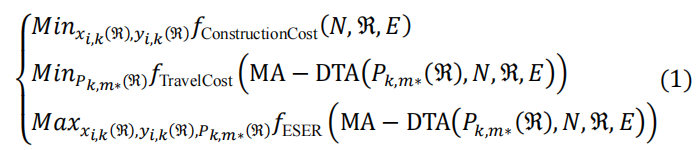
s.t.

在本研究中, 𝑂 和𝐷 是起点和终点(OD)的集合, 𝑜 ∈ 𝑂, 𝑑 ∈ 𝐷. 𝐼是服务区域的集合,𝑖 ∈ 𝐼, 𝑀是车辆类型的集合, 𝑚 ∈ 𝑀 ={ℎ, 𝑒} ,其中ℎ 指的是 GV, 𝑒 指的是 EV。𝑍是电力类型的集合, 𝑧 ∈ 𝑍 = {𝑔,𝑓} 。它包括TP 𝑓 和 GP 𝑔 ,其中原材料分别由煤炭和核能表示。为了简化问题,任何电站的电力仅由一种类型的电力供应。 𝐾 表示规划阶段的集合,𝑘∈ 𝐾 ={1,2, … , 𝑘max}. ℜ, 𝑁, 𝐸分别是充电、高速公路和配电网络。阶段𝑘 中充电站和充电桩的最优部署方案表示为𝑋′′𝑌′′,𝑈𝑘,𝑖(ℜ) 是设施利用率,指的是在阶段𝑘中全天在ℜ 布局下充电站𝑖 状态的平均值, 𝛽𝑧,𝑢𝑝, 𝛽𝑧,𝑑𝑜𝑤𝑛 是电力𝑧中设施利用率的上限和下限。𝐼zk(ℜ)是阶段𝑘 中在ℜ 布局下电力𝑧 中的充电站集合。 𝐿ek,o,d(𝑁, ℜ) 是阶段𝑘中在(N, R)网络上 EV 之间的有效路线集合,𝑦min是单个充电站的最小充电桩数量。
如公式(1)所示,该模型包含三个优化目标。第一个目标函数是最小化充电网络的建设成本。它取决于 𝑥𝑖,𝑘(ℜ) 和𝑦𝑖,𝑘(ℜ) ,其中𝑥𝑖,𝑘(ℜ) 是判断在ℜ 布局下第𝑘 阶段是否在服务区𝑖 建设充电站的二元变量。如果是,则𝑥𝑖,𝑘(ℜ) = 1 ,否则𝑥𝑖,𝑘(ℜ) = 0 。而𝑦𝑖,𝑘(ℜ) 是对应的充电桩数量。 𝑦′′ i,k+1是第𝑘 + 1 阶段站点𝑖 的最优容量。第二个目标是最小化电动汽车用户的出行成本。决策变量𝑃𝑘,𝑚∗(ℜ) 是𝑚∗ 选择路径𝑙 的概率,它决定了电动汽车用户的出行和充电过程。 𝑚∗是𝑚∗ = mo,d,t,l的缩写,表示在时间𝑡出发并选择通过(o, d)的路径𝑙 的类型𝑚 的车辆。第三个目标是最大化政府感兴趣的网络的ESER 效益。出行成本和ESER 效益通过 MA-DTA 模型计算,该模型动态模拟交通流传输和充电网络的运行。
同时,为了保证可持续运营和建设经济性,提出了不同电力区域设施利用率的约束条件,如公式(2)所示。公式(3)描述了有效路径集𝐿ek,o,d(𝑁, ℜ) 和空集⌀ 之间的关系。它保证了网络的可达性,即在极端条件下(在可容忍的SOC 限制下,其中𝑆exp =𝑆0k, 𝑆1 = 0 和𝑆2 = 0 ),电动汽车是否能够在任何OD 对之间实现城际旅行。公式(4)和(5)提出了充电站位置和容量的逆向建设约束。
3.2 挑战与应用难题
复杂多目标优化问题的解决方案大多使用启发式算法来获得帕累托前沿。然而,由于以下三个棘手的挑战,扩展到现实世界中的大规模网络在技术上是不可行的。
首先,由于该模型整合了运营和规划的概念,涉及多种变量。在规划层面,决策变量是充电站的位置和容量。在运营层面,它涉及电动汽车用户的出行和充电决策,以及电动汽车、道路网络和充电网络的实时状态。其次,大规模的高速公路和巨大的 交通流量将导致现实规划场景中的变量数量庞大。例如,一条高速公路有 40 个服务区,每天有 10 万辆汽车,电动汽车渗透率 为 20%。假设充电桩的最小和最大阈值分别为 4 和 20。估计有超过40x(20-4)×(100000×20%)=1280 万个决策变量。而系统中的实时状态变量的数量远远超过这个数量级。第三,多阶段整体规划导致变量数量呈指数增长,从而导致求解时间爆炸。
由于上述问题,即使在可接受的时间内获得合理的解决方案也很困难,即使对于启发式算法也是如此。因此,一些分解技 术,如运营分解和迭代或逐步方法,是使模型可解的必要条件。然而,以下建模挑战阻碍了运营分解的应用。由于电动汽车的异质性(由OD、出发时间、旅行路径和电池健康状况引起),途中充电需求在时间、位置和充电量方面各不相同,这使得通过数 学建模估计电动汽车的动态需求具有挑战性。通常,充电服务被简化为数学排队模型,例如 D/D/S 系统。它需要确定的到达率和服务率,这对于具有差异化充电需求的服务过程来说,推导出连续的闭式函数是具有挑战性的。相比之下,迭代或逐步规划方法的结构由多个通过数学逻辑关系连接的子模块组成。这些子模块可能以各种形式存在,例如数学优化模型、逻辑判断模型、数据驱动或多智能体模拟模型等。这种结构允许在迭代或步骤中考虑更多因素,例如本问题中的充电站运营。
基于上述讨论,为解决大规模多阶段EFCS部署问题,提出了一种基于迭代的规划方法
4. 规划方法
本节提出了一种三步规划方法,用于解决大规模多阶段EFCS 部署问题,基于“网络构建→ 需求估计→ 网络评估→ 部署优化”的设计思想。图 3 展示了规划阶段𝑘 下所提出方法的框架。
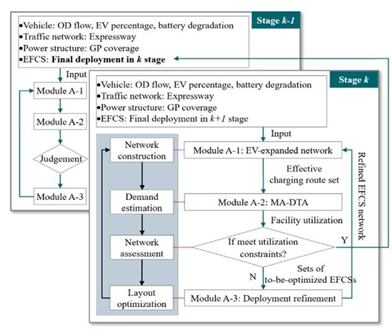
图 3 所提出方法的框架。
模型输入包括阶段𝑘 的 OD 流量、交通网络、GP 覆盖范围、高速公路以及阶段𝑘 + 1 中获得的最终 EFCS 部署。基于高速公路和充电网络,模型A-1 构建了有效的充电路线集,考虑了电动汽车用户的多次途中充电需求。为了实现“需求估计”,模型 A-2 中提出了一个 MA-DTA 模型,用于估计电动汽车用户的动态充电需求响应,并动态模拟交通流传输和充电站运营。在“网络评估”阶段,判断模块根据模型 A-2 输出的设施利用率获取待优化的 EFCS 集,并将其传递给模型A-3。这些充电站的位置和容量在提高ESER 效益和合理化设施利用率的指导下进行优化。进一步,优化后的EFCS 部署返回到模型A-1。当所有站点的利用率都在合理范围内时,迭代结束。最后,阶段𝑘 的最终部署输出到阶段𝑘 − 1 的模型中,以便逐步逆向规划充电网络。
接下来,详细描述了每个子模块的建模和功能。
4.1 模块 A-1:电动汽车扩展网络
在模块A-1 中,开发了 GV 和EV 的有效行驶路线集,为下一步提供数据基础。基于当前的高速公路、EFCS 部署以及上述四个SOC 阈值,构建了 GV 和 EV 的路线搜索算法,并将其调制为非线性函数,即𝐿ho,d(𝑁) =𝑓ℎ(𝑁, 𝛺) 和𝐿eo,d(𝑁, ℜ) =𝑓𝑒(𝑆0, 𝑆exp, 𝑆1, 𝑆2, 𝐿ho,d(𝑁), ℜ, 𝑛)。具体步骤如下:
步骤 1:基础路线集的构建。根据高速公路的拓扑结构,依次使用 Dijkstra 算法和改进的深度优先算法来获取最短路线集𝐿shortesto,d(𝑁) 和所有路线集𝐿𝑎𝑙𝑙o,d(𝑁) 。
步骤 2: 𝐺𝑉 有效路线集 𝐿ho,d的构建。基于𝐿shortesto,d(𝑁) 和𝐿𝑎𝑙𝑙o,d(𝑁) ,引入放大因子𝛺 ,并将长度小于𝛺 ∙ 𝐿shortesto,d(𝑁) 的路线视为GV 的有效路线集。
步骤 3:EV 有效路线集 𝐿ek,o,d(𝑁, ℜ) 的构建。
步骤 3.1:设置途中充电的最大次数𝑛 。根据高速公路的拓扑结构和 EV 的行驶里程,预设途中充电的最大次数𝑛 。此时,EV 用户可以在旅途中充电 0,1, … , 𝑛 次。
步骤 3.2:EV 充电路线备选集的构建。首先,基于GV 有效路线集𝐿ho,d(𝑁)和EFCS 部署ℜ ,获取EV 行驶路线和充电路线集。例如,GV 行驶路线表示为{𝑜, 𝑑1, 𝑑2, … 、 𝑑𝑥, 𝑑},其中𝑜, 𝑑1, … , 𝑑𝑥 是途中经过的收费站。通过在 GV 路线上添加经过的充电站{𝑐1, … , 𝑐𝑖, … , 𝑐𝑛},得到EV 行驶路线{𝑜, 𝑑1, 𝑐1, … , 𝑐𝑖, … 、 𝑐𝑛, 𝑑𝑥, 𝑑} 。{𝑜, 𝑐1, … , 𝑐𝑖 、… , 𝑐𝑛, 𝑑}是充电路线,由OD 和GV 路线上经过的充电站组合而成。然后,根据充电站的顺序列表和途中充电的最大次数𝑛 ,通过排列组合形成总共∑min(𝑛,𝑚)𝑖=0个EV 充电路线备选集。
步骤 3.3:充电路线有效性的判断。根据第 2.1.1 节的描述,充电路线{𝑜, 𝑐1, … , 𝑐𝑖, … , 𝑐𝑛, 𝑑} 需要满足以下三个距离约束:(1) 考虑𝑆0k 和𝑆1 ,从起点到第一个充电站的距离需要满足𝛥𝑑(𝑜, 𝑑1) ≤ 𝑙1 ;(2) 考虑𝑆exp 和𝑆2,途中任何两个连续经过的充电站之间的距离需要满足𝛥𝑑(𝑐𝑖, 𝑐𝑖+1) ≤ 𝑙2 + 𝑙3 ;(3) 考虑 𝑆exp 和𝑆1 ,从最后一个充电站到目的地的距离需要满足𝛥𝑑(𝑐𝑛, 𝑑) ≤ 𝑙3 。只有满足上述条件的路线才能被视为电动汽车的有效充电路线。
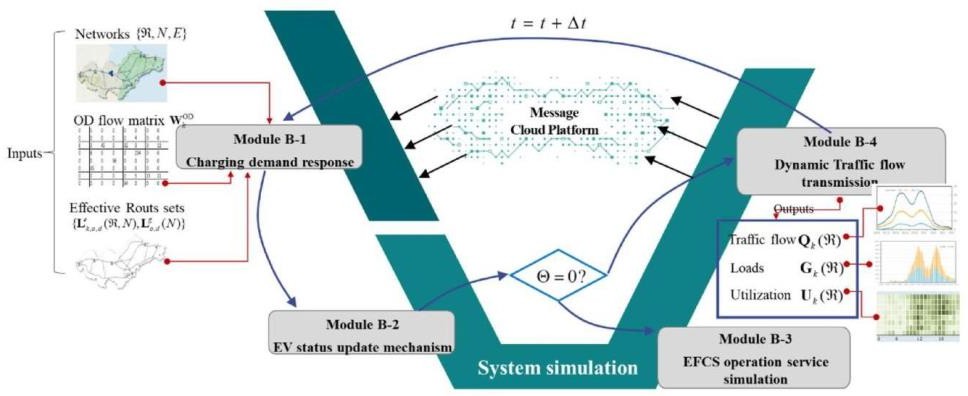
图 4 提出的基于多智能体的动态交通分配(MA-DTA)框架
4.2 模块A-2:MA-DTA
在模块A-2 中,高速公路、充电网络和混合交通流的实时状态被准确且全面地监控,这对于评估EFCS 部署和找到优化方 向至关重要。MA-DTA 模型由两层组成,即代理决策层(模块 B-1:充电需求响应)和系统模拟层(模块 B-2:电动汽车状态更新机制;模块B-3:EFCS 操作服务模拟;模块B-4:动态交通流传输)。图 4 展示了模块之间的交互。
在 MA-DTA 中,代理的充电需求响应在模块B-1 中呈现。代理的旅行路线决定了途中充电的位置,该路线在出发时基于路径大小logit(PSL)模型选择。在系统模拟层中,模拟了车辆、充电桩和网络的系统全天运行。具体来说,根据电动汽车的实时 状态更新(模块B-2),分别执行充电状态下的电动汽车的充电站操作服务(模块B-3)和驾驶状态下的电动汽车的动态交通流传输 (模块B-4)。在每个周期结束时,系统中的多个实体信息,包括车辆、充电桩和道路,都会实时上传到消息云平台。然后,这些信息通过移动通信设备同步到电动汽车,为它们的充电路线决策提供准确、实时和多样的信息。
为了表示 MA-DTA 模型在提出的三步规划方法中的功能定位,它被表述为一个非线性和高度非凸的函数, 𝛯 MAS-DSUE (∙) ,其输入和输出形式如下。
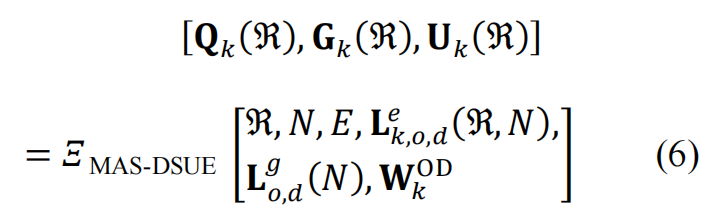
其中𝐖OD 𝑘是阶段𝑘 中的 OD 旅行矩阵。通过模拟,输出了三个三维时空状态矩阵𝐐𝑘(ℜ)、𝐆𝑘(ℜ) 、 𝐔𝑘(ℜ) ,它们分别表示阶段𝑘 下充电网络ℜ 的交通流量、充电负荷和设施利用率。并且, 𝐔𝑘(ℜ) 是模块A-3 中设施部署优化的关键决策指标。
(1) 模块B-1:充电需求响应
在出发时间,电动汽车用户必须决定行驶路线、是否充电以及在哪里充电,即充电路线。依靠消息云平台,用户可以在出发时掌握完整的实时交通网络信息(即每个路段的拥堵情况和预计行驶时间)和充电网络信息(即每个充电站的排队长度和预计最短排队时间)。根据Wardrop 的第一原则,所有用户选择自己估计的旅行成本最低的路线。最终,交通网络达到随机动态用户均衡(SDUE)状态,表示如下:
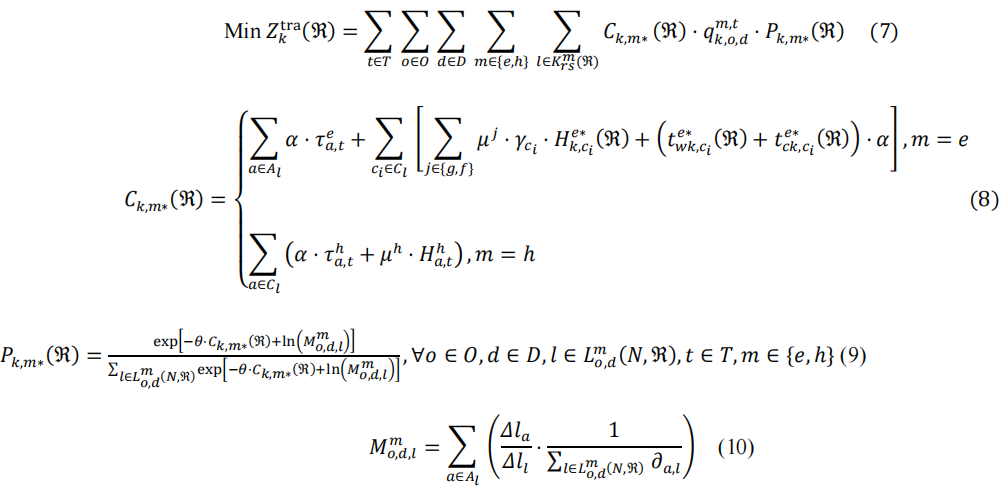
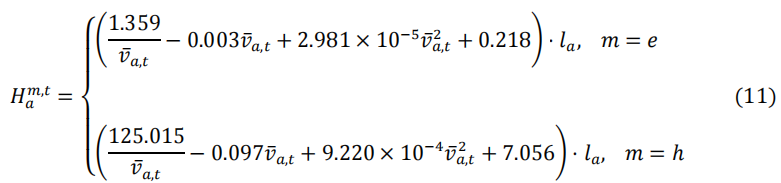
其中𝑍tra𝑘 (ℜ) 是阶段𝑘下充电网络ℜ 中车辆的总旅行成本, 𝐶𝑘,𝑚∗(ℜ)是𝑚∗的旅行成本. 𝑞𝑚,𝑡𝑘,𝑜,𝑑是𝑡时刻(o, d) 之间的新流量,𝛼是时间价值, 𝜇𝑔, 𝜇𝑓和𝜇ℎ是GP, TP和汽油的能源价格, 𝛾𝑐𝑖表示充电站𝑖 的供电类型,𝐻ℎ𝑎.𝑡是GVs第t 时刻在道路𝑎上的能耗,𝐻𝑒∗𝑐𝑖是充电站𝑖上𝑒∗的需求,𝑡𝑒∗𝑤𝑘,𝑐𝑖(ℜ)和𝑡𝑒∗ck,𝑐𝑖(ℜ)是在充电站𝑖上𝑒∗的排队时间和充电时间,𝜃是反映用户感知差异的离散系数,𝑀𝑚o,d,l是类型𝑚车辆通过(o, d)的路径𝑙的修正项,𝑙𝑎和𝑙𝑙分别是道路𝑎和路径𝑙 的长度,其中𝜕𝑎,𝑙是一个二元变量, 𝜕𝑎,𝑙 = 1 表示道路𝑎是路径𝑙的一部分,否则𝜕𝑎,𝑙 = 0。
如公式(7) 所示,MA-DTA 的目标是最小化 GVs 和 EVs 的总旅行成本。方程(8) 说明了GV 和 EV 的旅行成本组成部分。具体来说,电动汽车的旅行成本包括旅行时间成本∑𝑎∈𝐴 𝛼 ∙ 𝜏𝑒𝑎,𝑡电力消耗成本![]() 以及排队和充电时间成本
以及排队和充电时间成本![]() 。汽油车的旅行成本包括旅行时间成本∑𝑎∈𝐴 𝛼 ∙ 𝜏h𝑎,𝑡 和汽油消耗成本∑𝑎∈𝐴 𝛽ℎ ∙ 𝐻ℎ𝑎,𝑡。方程(9) 和(10) 计算了路线选择的概率。参考燃料消耗模型(Yao & Song, 2013),GV 和 EV 的能源消耗可由方程(11) 计算。
。汽油车的旅行成本包括旅行时间成本∑𝑎∈𝐴 𝛼 ∙ 𝜏h𝑎,𝑡 和汽油消耗成本∑𝑎∈𝐴 𝛽ℎ ∙ 𝐻ℎ𝑎,𝑡。方程(9) 和(10) 计算了路线选择的概率。参考燃料消耗模型(Yao & Song, 2013),GV 和 EV 的能源消耗可由方程(11) 计算。
(2) 模块B-2: 电动汽车状态更新机制
在 MA-DTA 中,每辆电动汽车都标记有两种信息。第一种是静态信息,即起点、目的地、行驶路线、充电路线和电池健康状态。第二种是随时间变化的动态信息,包括实时SOC、位置、电动汽车的工作状态𝛩 以及结束当前状态的剩余时间。
电动汽车的工作状态有两种:行驶状态𝛩 = 1和充电状态𝛩 = 0。充电状态指的是电动汽车进入充电站后的过程,包括排 队和充电。仿真系统使用滑动时间窗口算法来计算和更新电动汽车结束其状态的剩余时间。它可以分为离开当前道路和当前充电站的剩余时间。Amiri 等人(2018) 明确描述了仿真时间范围内时间窗口移动的范式。当更新的𝛩从 1变为 0时,电动汽车从高速公路移动到充电站以接受充电服务,具体过程在模块B-3 中描述。当更新的𝛩从 0变为 1时,电动汽车离开充电站并继续在高速公路上行驶,具体过程在模块B-4 中描述。
(3) 模块B-3: EFCS 操作服务仿真
在模块B-3 中,模拟了为具有离散到达和充电量异质性的电动汽车提供的EFCS 操作服务。对于充电站,静态属性包括位置、容量和电源类型;动态属性是每个充电桩的剩余运行时间。
对于到达的电动汽车,其状态从 1 切换到 0,并选择剩余运行时间最短的充电桩进行排队和充电,方程(12)中,电动汽车充电状态的结束时间,即所选充电桩的工作结束时间,由排队时间和电池充电时间决定。如方程(13)所示,排队时间等于充电站中所有充电桩在当前时间的最小剩余工作时间。如方程(14)所示,充电时间基于J.A.Mas 的可接受电流定律(Mas 等,1972)计算。
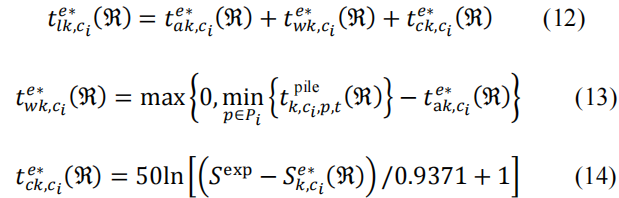
其中𝑡 pile𝑘,𝑐𝑖,𝑝,𝑡 (ℜ) 是充电站𝑖 在阶段𝑘下充电网络ℜ 中充电桩𝑝 在时间𝑡 的工作结束时间,![]() 和𝑡𝑒∗𝑐𝑘,𝑐𝑖(ℜ) 分别是𝑒∗ 在阶段𝑘 下充电网络ℜ 中充电站𝑖的到达、离开、等待和充电时间。 𝑆𝑒∗𝑘,𝑐𝑖(ℜ) 是𝑒∗ 在阶段𝑘 下充电网络ℜ中到达充电站𝑖时的SOC。
和𝑡𝑒∗𝑐𝑘,𝑐𝑖(ℜ) 分别是𝑒∗ 在阶段𝑘 下充电网络ℜ 中充电站𝑖的到达、离开、等待和充电时间。 𝑆𝑒∗𝑘,𝑐𝑖(ℜ) 是𝑒∗ 在阶段𝑘 下充电网络ℜ中到达充电站𝑖时的SOC。
(4) 模块B-4:动态交通流传输
在模块B-4 中,基于动态交通流传输模型模拟了高速公路上交通流的传输过程。车辆在传输过程中遵循先进先出原则。道路上的交通拥堵通过点排队模型进行估计。需要注意的是,由于充电站与高速公路相对隔离并通过匝道连接,接受充电服务的电动汽车不被视为交通负荷。由于篇幅有限,此处忽略了对DTA 模型的具体描述。模拟期结束后,更新的路网信息被传递到消息云平台,包括道路的交通负荷和旅行时间。将连续平均法应用于上述模拟环境,能够快速求解 MA-DTA,该方法能有效解决 SDUE 模型。
最后,为了展示 MA-DTA 在电动汽车途中充电服务中提出的“动态”特性的适用性,表 1 详细列出了 MA-DTA、传统 DTA和排队理论之间的差异。
4.3 模块A-3:优化策略
基于模块A-2 的动态模拟,包括电动汽车和充电桩在内的多智能体的日常状态被汇总用于网络评估。然后,EFCS 网络被优化以提高ESER 效益并合理化设施利用率。
4.3.1 网络评估
评估指标可以分为两大类:LOS 和ESER 效益。
充电网络服务:充电网络的 LOS 是电动汽车用户的主要关注点。平均等待和充电时间基于方程 (13) 和 (14) 的汇总获得。设施利用率𝑈𝑘,𝑖(ℜ) 通过方程(15) 计算。它反映了充电站供需的动态水平。
![]()
其中𝑆′是时间部分的数量。 𝑞𝑘,𝑐 ,𝑡(ℜ)/𝑦𝑘,𝑖(ℜ) 表示在时间𝑡 时充电站𝑖 的车辆数量与充电桩数量的比率,即每个时间步结束时充电桩的平均占用率。当𝑞𝑘,𝑐𝑖,𝑡(ℜ)/𝑦𝑘,𝑖(ℜ) = 1 时,意味着所有充电桩都在工作,所有电动汽车都在充电。 𝑈𝑘,𝑖(ℜ) 越高,充电站𝑖的工作量越大。
ESER 效益:政府重视车辆电气化和 PS 转型带来的 ESER 效益。因此,提出了三个指标,包括标准煤(SC)节约、 CO2 减排(CER)和GP 百分比。
𝑆𝐶节约:SC 节约指的是 PG 减少的总 SC。考虑到由于排队时间过长而导致的电动汽车损失,只有排队时间小于 𝜓 的电动汽车的充电请求被视为完成的充电服务。TP 和GP 的有效电力消耗通过公式(16)计算。
![]()
其中𝐸 actual ,z𝑘(ℜ) 和𝐸z𝑘(ℜ) 是实际PG 和该地区所有充电需求,功率为𝑧 。
然后,将来自TP 和 GP 的实际电力来源转换为 SC 以计算节能,如下所示
表 1 基于多智能体的动态交通分配(MA-DTA)、动态交通分配(DTA)和排队理论的功能列表。

![]()
其中 𝐸𝑁𝐺 𝑧𝑘(ℜ) 是在功率为𝑧 的区域中提供等效能量所需的SC 数量, 𝜉e 是 SC 的功率系数。
CO2 减排:为了评估环境效益,提出了两个指标,分别在公式(17) 和 (18) 中。 𝐶𝐸𝑅𝑃𝐺(ℜ) 指的是通过车辆电气化实现的CER,即在等效行驶里程下将汽油转换为电力所节省的CO2 。 𝐶𝐸𝑅𝑃𝑆𝑇𝑘(ℜ) 指的是通过 PS 转换实现的CER,通过用GP 替换TP来提供等效能量来计算。
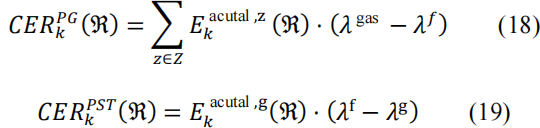
其中𝜆 gas , 𝜆f 和𝜆𝑔 分别是汽油、TP 和GP 的碳排放因子。
GP 的百分比:GP 百分比指的是 GP 发电量占总PG 的比例。然后,实际GP 百分比和标准化GP 百分比计算如下。
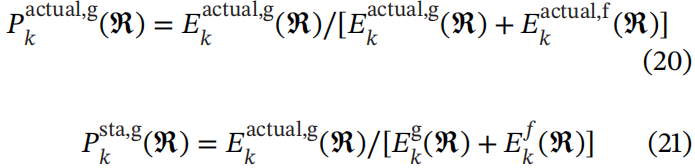
![]()
其中𝑃 actual ,g𝑘(ℜ) 表示考虑 EV 损耗的网络中实际GP 百分比。然而,由于分母不同,很难横向比较不同EFCS部署下的GP百分比。因此,提出了标准 GP 百分比𝑃 sta, g𝑘(ℜ) ,表示 GP 的有效PG 占网络中总电力需求的比例。要注意的是,当网络LOS 达到足够高的水平时,即所有 EV 的排队时间都小于𝜓 时, 𝑃 actual ,g𝑘(ℜ) 和𝑃 sta, g𝑘(ℜ) 的值相等。
4.3.2 部署优化
优化策略旨在提高ESER 效益和 EFCS 网络的设施利用合理性,同时保障其网络可达性和有序建设。基于贪心策略,每次迭代中进行局部最优的部署优化,以期在每个规划阶段找到全局最优解。
其伪代码如表 2 所示。首先,根据设施的工作状态找到待优化的充电站及其优化方向(第 1 行)。基于公式(2),构建了四个待优化的充电站集合𝐺𝑔,𝑒𝑥𝑘(ℜ), 𝐺𝑓,𝑒𝑥𝑘(ℜ) 、 𝐺𝑔,𝑢𝑛𝑘(ℜ) 和𝐺𝑓,𝑢𝑛𝑘(ℜ) 。它们分别表示 GP 区域和 TP 区域中设施利用率高于和低于阈值的充电站集合。
接下来,采用反向消除方法对网络中的待优化站点进行优化,以避免高负载并消除设施冗余。一方面,当利用率超过上限阈值时,表明该站点负载较高,全天保持稳定合理的服务水平(LOS)具有挑战性。优化策略是在每次迭代中为𝐺𝑔,𝑒𝑥𝑘(ℜ)或𝐺𝑓,𝑒𝑥𝑘(ℜ)中的所有站点增加一个充电桩单位(第 2-8 行)。优化策略设置了差异化的部署优化优先级,以挖掘 PS 转型带来的网络 ESER 效益。它优先提升 GP 区域内充电设施的服务能力(第 2-5 行)。当且仅当 GP 区域内所有站点的利用率满足公式(2)时,进一步优化 TP 区域内的服务能力。另一方面,当利用率低于下限阈值时,表明该站点全天工作负荷较低,存在设施冗余。在这种情况下,通过消除充电站(第 10-14 行)或每次迭代减少一个充电桩单位(第 15-18 行)来优化设施配置。在优化阶段,充电网络需要满足网络可达性约束公式(3)以及前向/后向建设约束公式(4)和(5)或公式(6)和(7)。当调整后的充电桩数量小于𝑦min 时,需要判断是否消除该站点。如果移除站点后仍满足公式(3),则移除该站点;否则保留。
表 2 优化策略的伪代码。

5.数值实验
在本节中,所提出的三步规划方法的有效性在Nguyen-Dupius 网络上得到了验证。如图 5 所示,该网络由 13 个道路节点(圆圈)和四个候选服务区(三角形)组成。
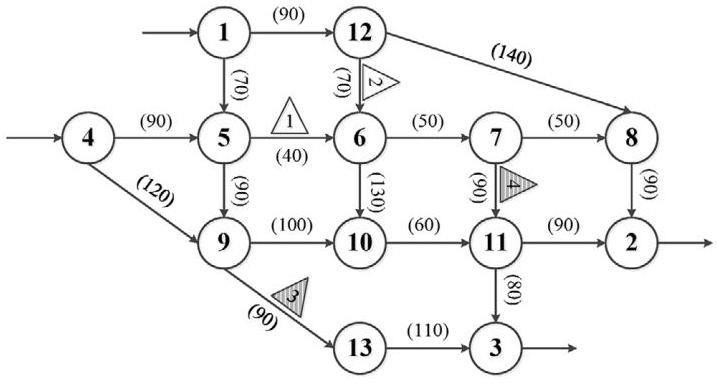
图 5 带有四个服务区的Nguyen-Dupius 网络
道路的长度由括号中的数字表示。道路的容量和车辆速度设置为 2300 pcu 和 100 km/h 。四个 OD 对的流量率:(1,2)、(1,3)、 (4,2)和(4,3)分别设置为 8、15、12 和 8 pcu/15min。候选服务区 1 和 2 位于 TP 区域,而服务区 3 和 4 位于 GP 区域。每个服务区在初始迭代中建有一个充电站,配备四个充电桩。参考 Zhang 等人(2022),一些参数设置如下: 𝛼 = 34RMB/h; 𝜃 = 1; 𝛽𝑔 =0.488RMB/km 。根据实际数据调查,一些参数设置如下: 𝛽𝑓 = 1.29RMB/KWh; 𝜉e = 0.324 g/KWh ; 𝜆gas = 27.6kg/100km; 𝜆f = 0.9644kg/KWh; 𝑦 min = 4; 𝜆𝑔 = 0.009kg/KWh。其他参数设置如下: 𝑆1 = 40%; 𝑆2 = 20%; 𝑛 = 2; 𝛺 = 1.5; 𝑆′ = 96; 𝜓 = 15 min ; 𝛽𝑔,𝑢𝑝 = 𝛽𝑓,𝑢𝑝 = 0.6, 𝛽𝑔, down = 𝛽𝑓, down = 0.15; 𝛽𝑔 = 0.8𝛽𝑓 。
在配置为Intel Core i7-8650U 1.90 GHz 和 16 GB RAM 的个人电脑上测试了六种情况(不同的服务区位置和电动汽车渗透率)。每种情况的解决方案列在表 3 中。首先,通过提出的三步规划方法获得最终解决方案,如“Solution”列所示。例如,[2:4; 3:7, 4:4]表示在服务区 2、3 和 4 分别建了 4、7 和 4 个充电桩。“Iter”列指的是获得最终解决方案的迭代次数。单个充电站充电桩的最大阈值设置为最终解决方案中单个充电站的最大充电桩数量。然后,枚举所有部署方案。“Num 1 ”是所有解决方案的数量。“Num2”是受方程(2)和(3)约束的可行解的数量。“Num3”是基于方程(1)中三个目标的非支配解的数量。“Num4”是最终获得的解决方案的支配解的数量。“Rank”是 Num3 + Num4 与 Num1 的比率。其含义是获得的解决方案在所有解决方案中的保守排名。“GPU”是找到最终解决方案的操作时间。
表 3 六种情况下的解决方案。

分析表 3,得出以下结论:(i) 在设施利用率和网络约束的共同作用下,模型大大减少了可行解的规模。在案例 2-6 中,可行解的比例仅为总解的 2.4%–8.0%。(ii) 尽管该方法难以获得所有最优解,但它可以获得高质量的可行解甚至最优解。在案例 2-6 中,获得的解排名在前 3.1%。(iii) 该方法通过迭代规划方法高效解决了所提出的多目标问题。如表 3 所示,随着备选点数量和电动汽车(EV)渗透率的增加,所有解决方案的数量急剧增加。在案例 2-6 中,迭代次数不到所有解决方案的 1%。这种高求解效率在大规模规划场景中至关重要。将在第 6.2.2 节中进一步讨论在实际规划场景中所提出的优化策略的效率。
6. 实验研究
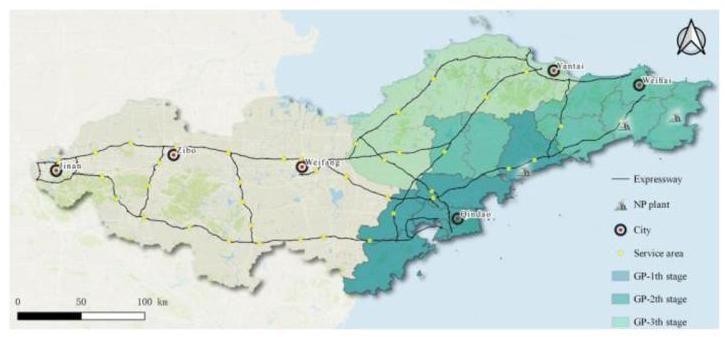
图 6 山东半岛高速公路。
选择山东半岛城市群作为实证研究对象。本案例中高速公路和 GP 发展计划的简要描述如下:
图 6描绘了山东半岛的高速公路,连接了济南、淄博、青岛和烟台等主要城市。网络总长度为 2187 公里,包含 169 个收费站、177 条道路和 39 个服务区。参考中国高速公路已建充电站的当前配置,初始迭代的EFCS 部署设置为在所有服务区建设一个配备四个充电桩的充电站。
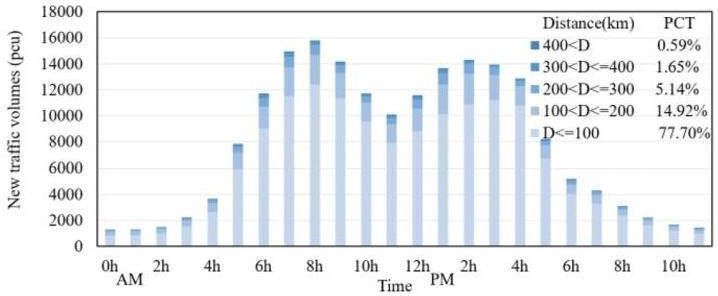
图 7 不同行驶距离下的交通量时间分布。
全天的网络交通流量为 188843 辆,采集间隔为 15 min 。图 7 展示了不同行驶距离下交通量的时间分布。城际出行主要集中在短距离范围内,其中 100 公里以内的出行占比高达 77.70%。而超过 200 公里的出行仅占 7.38%,这表明在高速公路上需要补充能源的车辆比例较低。
目前,山东半岛正在建设核电集群,以大规模和高比例推动非化石能源的发展。2021年,山东的年发电量为 5808 亿千瓦时,其中 5217 亿千瓦时由 TP 供应,占总量的 90%。因此,山东省计划在胶东半岛建设一个 10 兆瓦的核电基地,以减少TP 发电的比例。核电每千瓦时仅排放5.7g 的碳,远低于煤炭的357 g 。根据计划,到 2025 年,运行和在建的核电装机容量将达到约 1300 万千瓦。它将逐步实现胶东半岛的核电供应。
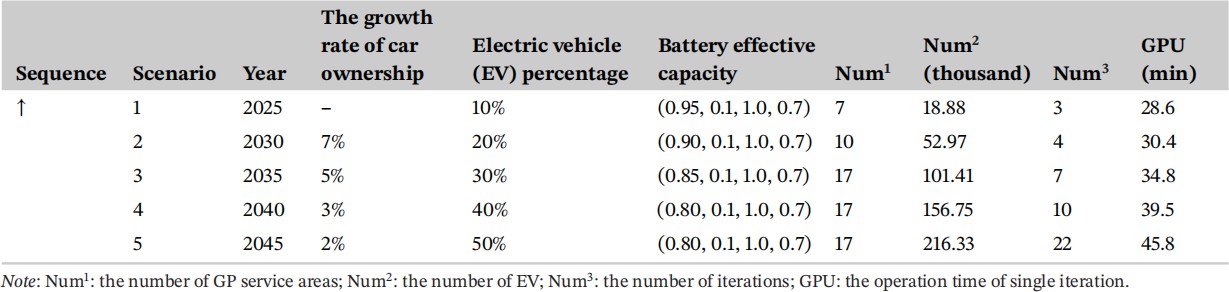
在本研究中,考虑到汽车保有量和电动汽车比例的增加、电池退化以及 GP 覆盖范围的扩大,设定了从 2025 年到 2045 年每 5 年一个规划情景,共五个情景,如表 4 所示。其中,汽车保有量的增长率是根据过去 10 年山东省私人车辆增长率的变化预测的。根据电动汽车市场的发展规划和基础设施“适度超前”的原则,电动汽车的比例分别设定为 10%, 20%, 30%, 40% 和 50%。电动汽车组的电池退化呈现出先下降后保持稳定的趋势,参数设置参考了Wang, Zhao 等人(2021)的研究。根据山东核电的发展规划,GP 覆盖范围设定为三个阶段。如图 6 所示,GP 覆盖的服务区数量分别为 7、10 和 17。参数设置与第 5 节相同。基于上述情景设置,所提出模型涉及的变量数量巨大。假设最大充电桩阈值为 20,充电站的决策变量数量为 39 × (20 − 4) × 5 = 3120 。估计约有 sum(Num2) = 546.35 千个电动汽车决策变量。设施利用率约束、网络可达性约束和反向建设约束的数量分别为 39 × 5 = 195 、 169 × 168 × 5 = 141,960 和 39 × 5 × 2 = 390 。由于网络规模大且交通流量大,单个部署方案的求解时间从 28.6min 到 45.8min 不等。在这种大规模规划情景中,即使启发式算法也难以在可接受的时间内获得满意的解决方案。
表 4 2025-2045 年情景的变量设置。
6.1 充电基础设施的部署方案
在本节中,以情景 5 为例,展示了迭代优化过程,以验证所提出的优化策略的有效性。同时,阐明了将运营与规划相结合的必要性,并进一步探讨了需求诱导效应。
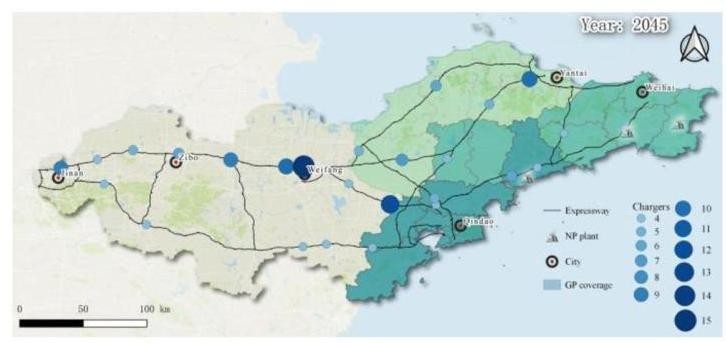
图 8 情景 5 的最终部署方案
6.1.1最终部署方案
在情景 5 中,经过 22 次迭代后获得了最终解决方案。如图 8 所示,EFCS 网络包括 26 个充电站,配备 157 个充电桩。TP 区域有 12 个充电站,配备 78 个充电桩,GP 区域有 14 个充电站,配备 79 个充电桩。
6.1.2优化策略的工作原理和效率
通过分析迭代过程中网络指标的变化,展示了所提出的优化策略在大规模规划场景中的工作原理和有效性,如图 9 所示。在网络建设规模方面,充电站数量显著减少,充电桩数量呈现快速下降后缓慢增长的趋势。通过第一次迭代,基本完成了网络中低效充电站的淘汰,共移除了 12 个充电站。根据所提出的优化策略中的优化优先级,第 2 至 9 次迭代是对 GP 区域充电桩配置的优化过程,直到设施利用率达到阈值条件。随后,算法对TP 区域的设施部署进行了优化。与当前布局相比,最终的 EFCS 网络布局更加高效合理。与当前布局相比,最终的电动汽车充电站(EFCS)部署方案得到了显著优化,淘汰了低效充电站,同时提升了关键站点的服务能力。
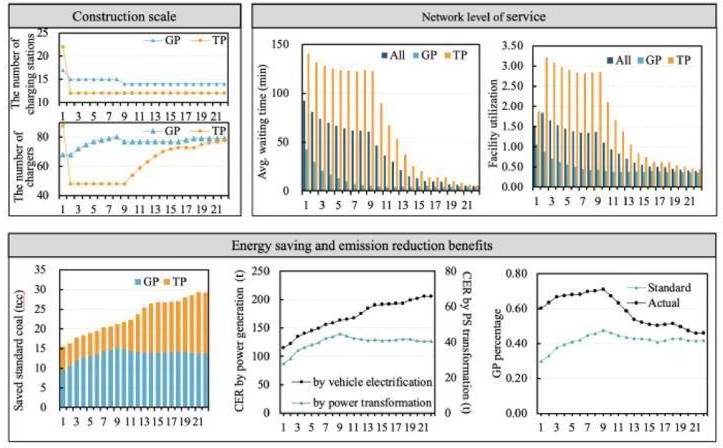
图 9 场景 5 中的迭代优化过程
在网络服务方面,充电网络的服务水平显著提高,电动汽车的平均等待时间和设施利用率在最终布局中达到了合理范围。当前布局中充电桩的平均分配导致服务水平较低,平均等待时间高达 92.52min,严重影响了城际出行。在前八次迭代中,GP区域的服务水平首先得到了显著改善,平均等待时间从 42.86min 迅速下降到 6.10min,利用率从 1.06 提高到 0.43。提高 GP 区域的服务能力可以缓解 TP 区域的部分负荷压力,但要满足其充电需求的高服务水平仍然具有挑战性。随着设施的进一步优化,最终网络服务水平达到了令人满意的水平,平均等待时间为 5.04min,设施利用率为 0.41。一方面,具有高服务水平的EFCS网络在保障电动汽车城际出行方面发挥了重要作用;另一方面,它有助于实现 EFCS 的可持续运营,并保护运营商的投资回报。
在能源和环境方面,随着EFCS 部署的优化,整体ESER 效益逐渐增加并趋于稳定。GP 百分比呈现先增加后减少的趋势。在前八次迭代中,随着 GP 区域设施配置的优化,GP 百分比及其ESER 效益不断增加。在第八次迭代后,标准 GP 百分比和实际 GP 百分比分别达到 48%和 71%,其每日 GP 发电量相当于节省了 15.72 吨 SC,减少了 44.68 吨 CO2 。随着TP 区域服务能力的提高,网络的整体ESER 效益继续增加。相比之下,GP 带来的效益不可避免地有所下降。与当前布局相比,最终EFCS 部署下车辆电气化节省的 SC 及其 CER 分别增加了 88.4%(15.5 吨-29.2 吨)和 78.5%(115.1 吨-205.5 吨)。同时,PS 改造也做出了显著贡献,其标准化百分比上升了 12.0%(30%-42%),CER 上升了 44.6%(27.85t − 40.27t) 。
总的来说,通过淘汰低效充电站并提升关键站点的服务能力,EFCS 网络的部署得到了显著优化。它显著提高了网络的LOS 和ESER 效益,保证了电动汽车的城际出行和设施的可持续运营,并为高速公路的低碳发展做出了贡献。
6.1.3 模拟充电服务过程的必要性
本节阐述了在 CFD 中模拟充电站运营的必要性。以下三种情况对充电站的服务过程进行了不同的建模。
1. NQ 案例:不考虑电动汽车在站点的排队过程(称为无排队[NQ]案例)。
2. QT 案例:第二种是排队理论(QT)案例,其中充电站被建模为一个数学排队系统。等待时间由![]() 计算,其中𝑡0 w𝑐𝑖是自由流的等待时间,这个预设参数选择了三个级别:2min、5min 和 10min。 𝑢 是站点中的电动汽车数量,𝐶𝑐𝑖 是充电站的服务能力,假设一个充电桩每小时可以为两辆电动汽车服务。
计算,其中𝑡0 w𝑐𝑖是自由流的等待时间,这个预设参数选择了三个级别:2min、5min 和 10min。 𝑢 是站点中的电动汽车数量,𝐶𝑐𝑖 是充电站的服务能力,假设一个充电桩每小时可以为两辆电动汽车服务。
3. MS 案例:通过提出的多智能体模拟方法(称为 MS 案例)考虑电动汽车的离散到达和充电站中的差异化充电需求。
将这三种情况代入提出的三步规划模型中,以获得每种情况下最终布局的实际运行状态,如表 5 所示。
表 5 三种情况下的部署比较。
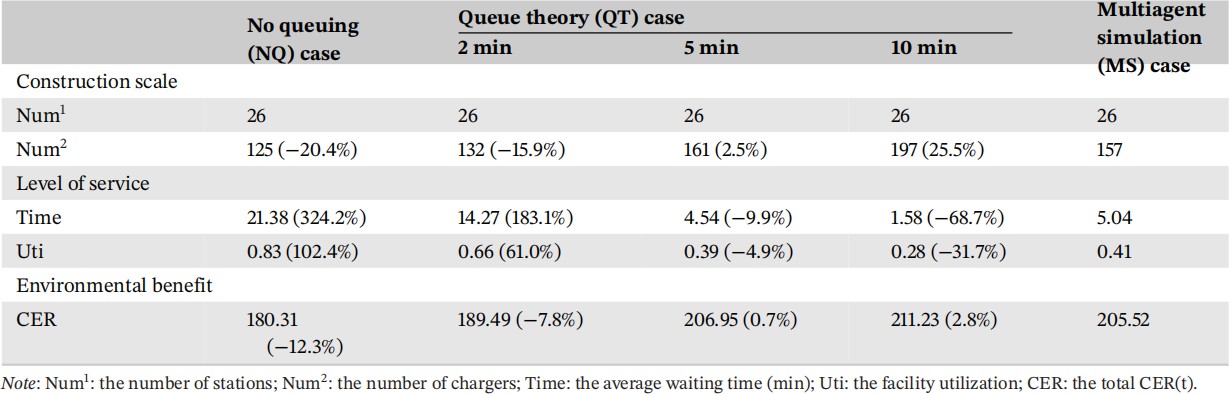
分析表明,充电服务模型对EFCS 的部署和运营有显著影响。过高的𝑢𝑐𝑖 值导致充电设施冗余,利用率降低。与 MS 情况相比,QT-10min 情况下过高的𝑢𝑐𝑖 设置使充电桩数量增加到197 个,增加了 25.5%。然而,更高配置带来的环境效益改善微乎其微,总 CER 仅增加了 2.8%。此外,设施利用率下降了31.7%。低𝑢𝑐𝑖 值或忽略排队会导致设施在实际运行中过载,难以维持全天可持续运行。这里是一个在 QT-2min 和 NQ 情况下LOS较低的EFCS 网络。NQ 和 QT-2min 情况下的平均等待时间分别达到 21.28min 和 14.27min,分别增加了 324.2%和 183.1%。相应的设施利用率达到 0.83 和 0.66,表明充电设施长期处于高负荷状态。同时,部署的减少导致 CER 显著下降,分别减少了12.3%和 7.8%。
6.1.4网络实时运行
此外,通过对网络和单个站点级别的实时充电负荷和设施运行状态的分析,说明了所提出的规划方法在整合运行和规划以确保设施可持续运行方面的重要性。
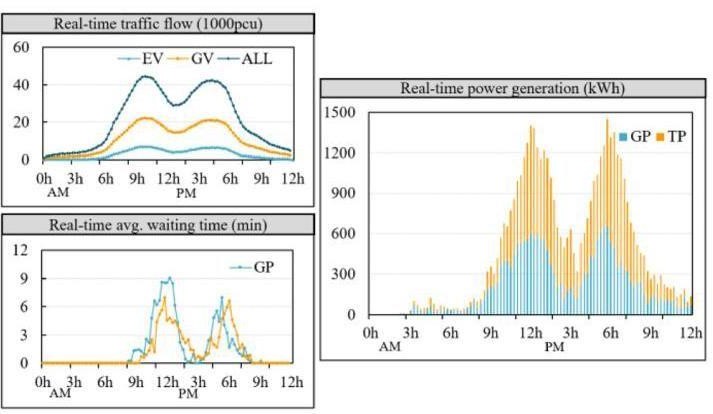
图 10 实时网络状态。
图 10 显示了全天交通流量、网络的服务水平(LOS)和 PG 的动态变化。在高速公路上,交通流量在 9:00 至 11:00 和 17:00至 19:00 之间出现了明显的双峰。在负荷方面,充电网络中等待时间和PG 的双峰相对于流量的双峰向后延迟了约 2 小时 ,这与电动汽车的能耗特性和行驶距离有关。从 9:00 到 20:00,充电网络处于工作饱和状态,有轻微的排队现象。GP 区域的充电负荷在 12:15-12:30 达到最大值,此时平均等待时间为 9.02min,PG 为877.66kWh。
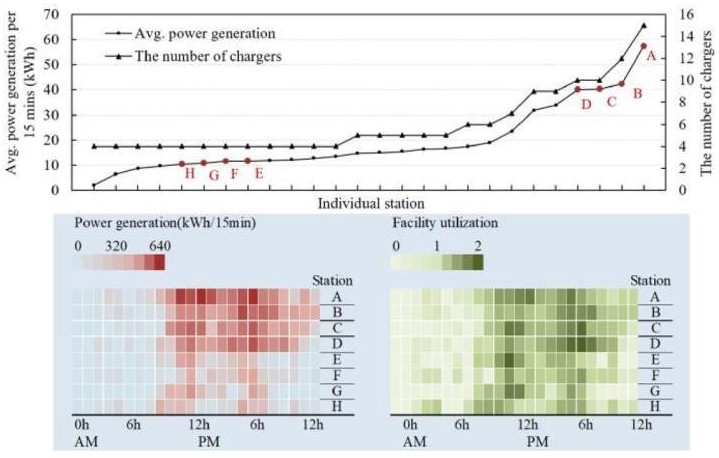
图 11 单个站点的供需匹配关系和实时运行状况。
接下来,分析了单个站点的供需匹配关系。在图 11 中,26 个充电站按平均能耗 15min 排序。它们的服务能力也显示出来。主要结果包括以下几点:(i) 充电站之间的负载差异显著,PG 范围从 1.979 kWh 到 57.36 kWh/15min。大约 70%的站点的 PG 集中在 6kWh − 20kWh /15min 范围内。(ii)每个充电站的服务能力与其负荷呈显著正相关。根据充电负荷的大小,每个充电站配置的充电桩数量从 4 个到 15 个不等。
此外,选择了四个充电功率较高的充电站(A、B、C、D)和四个充电功率较低的充电站(E、F、G、H)进行比较分析。观察到:(i) 在 11:00-20:00 期间,站点A、B、C 和D 的充电负载显著高于站点E, F, G 和H ,但实时利用率的差异较小。(ii) 在高峰时段,所有站点的利用率大多保持在[1,2] 范围内,具有“高饱和度和低排队”的特点。低负载站点的利用率在高峰时段保持在 1 左右,表明大多数充电桩处于工作状态,保证了站点的经济性。高负荷充电站仅在少数时段利用率接近 2,此时每个充电桩最多只有一辆电动汽车在排队,从而保证了充电站的服务水平(LOS)。
综上所述,所提出的三步规划方法实现了运营与规划的有机结合。通过多智能体动态交通分配(MA-DTA)模型,将运营层面对充电网络负荷和运行状态的实时监控与评估功能,以及规划层面对设施资源的部署优化功能相结合。该方法能够根据动态充电负荷有效分配设施资源,使每个充电站的实时服务水平和利用率保持在合理范围内,避免资源冗余或短缺。
6.1.5 需求诱导效应
本研究探讨了经济诱导方法和设施诱导方法的需求诱导效应。在经济诱导方法中,设定了不同的充电价格;在设施诱导方法中,采用了两种方式:一是设定不同的部署优化优先级,二是设定不同的服务水平(LOS)。具体设置了以下七种案例:
案例 1:没有需求诱导方法,即 TP 和 GP 充电价格相同,每个区域的部署细化优先级相同。
案例 2:设置差异化充电价格,其中 𝛽𝑔 = 0.8𝛽𝑓。
案例 3:设置差异化部署优化优先级,如表 2 所示(第 2 行-第 5 行)。
案例 4-7:设置差异化充电价格和部署优化优先级。利用阈值参数是确定充电网络在拟议优化策略中的 LOS 的关键指标。因此,使用差异化LOS 方法, 𝛽𝑓,𝑢𝑝 的值设置为四个级别,分别为 0.6、0.8、1 和 1.5。
各种案例中的部署方案性能如图 12 所示。案例 1 和 2,以及案例 3 和 4 的比较表明,差异化充电价格在诱导EFCS 网络需求方面效果较差。这是因为充电价格调整对电动汽车用户充电路线的效用影响较小。此外,如案例 1 和 3,以及案例 2 和 4 的比较所示,差异化部署优化优先级通过优先提升 GP 区域站点的服务能力,显著提高了网络的ESER 效益。以案例 1 和 3 的比较为例,实施优化优先级策略增加了 GP 区域的服务能力,相应地,网络的 CER 增加了 5.02%。
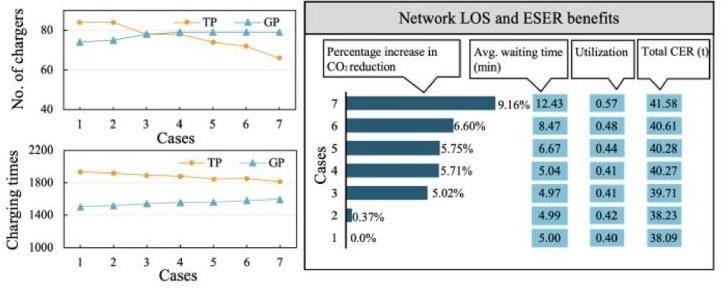
图 12 各种案例中的部署方案性能。
𝛽𝑓,𝑢𝑝 的增加导致不同区域设施 LOS 的不平衡,影响电动汽车用户的充电选择和网络的ESER 效益。随着𝛽𝑓,𝑢𝑝 从 0.6 增加到 1.5,TP 和 GP 区域内充电桩数量的差异逐渐从 1 增加到 13。这导致网络的总 CER 提高了3.45%。同时, 𝛽𝑓,𝑢𝑝 的增加不可避免地导致网络的 LOS 下降。当𝛽𝑓,𝑢𝑝 从 0.6 增加到 1.5 时,平均等待时间从 5.04min 增加到 12.43min 。因此,规划者在希望通过差异化LOS 方法诱导需求时,应协调网络的服务水平和ESER 效益。
6.2充电基础设施的动态部署方案
根据表 4 中提出的五种情景,探讨了 2025-2045 年EFCS 部署和网络指标的动态变化作为基准案例。
6.2.1动态部署方案
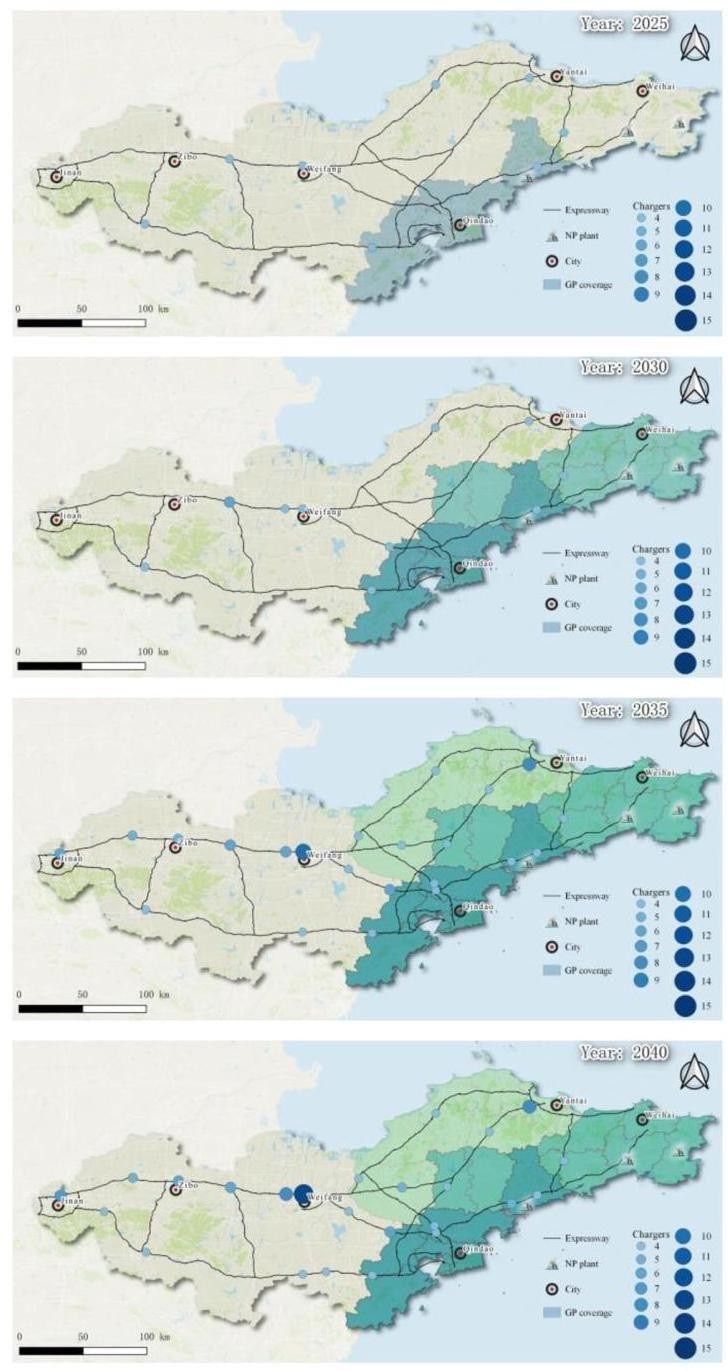
图 13 各阶段的最终部署方案。
图 13 显示了获得的动态部署方案,主要结论如下:
1. 在初始阶段(情景 1 和 2),充电站将主要建设在主要城市之间的中心道路上,以最大化充电站的服务覆盖范围。在情景 1中,配置了最少数量充电桩的 8 个充电站共同构成了满足电动汽车城际出行可达性的基础充电网络。
2. 2035 年是关键规划期,届时山东半岛的EFCS 网络最终部署基本形成。在 2030 年至 2035 年期间,EFCS 网络的规模将大幅扩展:充电站数量将从 10 个增加到 23 个,充电桩数量将从 42 个增加到 112 个。在后续发展中,EFCS 布局基本保持不变。
3. 随着 EFCS 布局的改善,后期规划主要集中在主要城市周边的服务区,以增强关键站点的服务能力。从 2035 年到 2045年,充电站数量仅增加三个,而每个充电站的平均充电桩数量从 4.87 个增加到 6.04 个。观察到,高配置的充电站主要位于主要城市周边,如济南、潍坊、烟台和青岛。这一现象表明,应在主要城市周边的服务区预留更多土地和电力供应系统,以扩大充电站的服务能力。同时,根据交通流量、经济和地理条件,可以创建一个集能源补充、购物、休闲和娱乐于一体的多功能商业综合体服务区,以缓解电动汽车用户因充电需求而产生的时间焦虑。
6.2.2动态网络指标
此外,分析了EFCS 网络在不同阶段的建设规模、LOS 和ESER 效益变化,统计结果如图 14 所示。
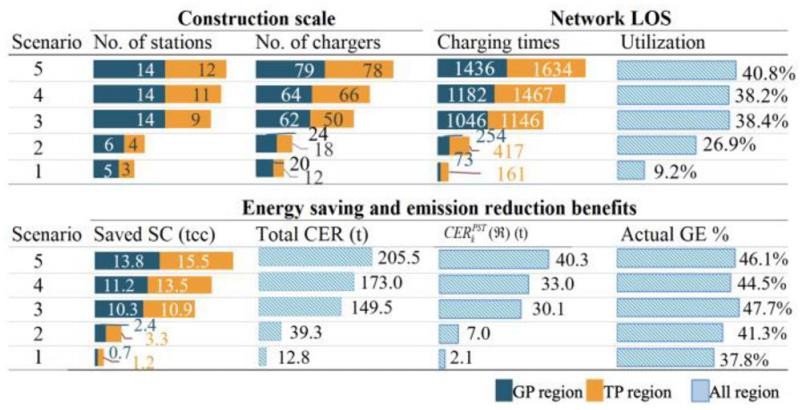
图 14 不同阶段部署方案的性能
建设规模和LOS:
通过合理的部署规划,随着电动汽车市场的增长,公共充电站“低利用率”的问题将得到解决。目前,“低利用率”现象广泛存在于公共充电站,尤其是在高速公路上。电动汽车城际出行量低和EFCS 布局不合理是造成这一现象的原因。随着电动汽车渗透率的增加和充电网络的有序建设,EFCS 网络将服务于更多的电动汽车用户,从 2025 年最初的每天 234 辆增加到 2045年的每天 3070 辆。设施利用率从 2025 年的 0.092 提高到 2030 年的 0.31,并在 2035-2045 年期间稳定在 0.38-0.40 的合理范围内。适当的设施利用率保证了电动汽车用户的出行满意度,并使EFCS 网络实现经济可持续性。
ESER 效益:
到 2035 年,电动汽车市场的发展和电力系统转型带来的ESER 效益将大幅提升。当电动汽车比例从 20%增加到 30%时,网络的全天 SC 节省从 5.7tcc 增加到 21.1tcc,增长了 270%;总 CER 从 39.3t 增加到 149.5t,增长了 280%。同时,当整个胶东半岛完成电力转型时,网络的ESER 效益将大幅提升。从 2030 年到 2035 年,网络的实际 GP 比例将从 23.7%增加到 47.7%,电力转型带来的CER 将从 5.6t 增加到 30.1t。
电力转型在促进交通脱碳方面具有重要意义。在 2025 年至 2035 年 GP 覆盖范围扩展期间,电力系统转型带来的 CER 从2.1t 增加到 30.1t。因此,不同地区应根据当地地理环境、经济发展和能源需求,发展光伏、风能、地热和核能等各种绿色能源。
6.2.3 网络可达性约束的必要性
表 6 NNC 和基线案例的性能比较

本节通过设置一个名为NNC(无网络可达性约束)的案例,展示了网络可达性约束的必要性。该案例未考虑公式(3)。表 6 列出了 2025 年至 2045 年期间 NNC 案例与基准案例的性能对比,括号内的数字表示NNC 案例中各指标相对于基准案例的百分比变化。
结果表明,网络可达性约束对EFCS 网络部署和运营的影响主要在早期阶段。在情景 4 和 5 中,NNC 案例中的最终EFCS部署与基线案例相同。与基线案例相比,NNC 案例中的充电站数量在 2025 年和 2030 年分别减少了 62.5%和 40.0%。设施利用率分别增加了 117.8%和 44.0%。这表明,在没有网络可达性约束的情况下,EFCS 网络在早期阶段更为经济。然而,在 2025 年和 2030 年,NNC 案例中有 11.5%和 7.7%的 OD 对对于 EV 用户来说是不可达的。这将限制 EV 出行的覆盖范围,并降低公众购买和使用 EV 的意愿。
7. 结论
本研究旨在为EFCS 的有序部署提供一种实用且合理的规划方法,并与区域电力结构(Power Structure, PS)的转型相协调。所提出的方法在数值实验中进行了测试,并应用于山东半岛高速公路的实证案例中。
结果表明,三步规划方法可以在可接受的计算时间内高效地获得高质量的解决方案,并适用于现实的规划场景。通过协调 充电基础设施部署与不均匀的 PS,该方法在增强 EFCS 网络的 ESER 效益方面是有效的。此外,实时充电负荷和设施状态表明,所提出的规划模型可以有效地分配设施资源,确保每个站的动态 LOS 和利用率合理。在高峰时段,站点状态为“高饱和低排队”,所有站点的实时利用率保持在[1,2] 范围内。这表明,整合运营和规划实现了网络的可持续全天候运营,有效避免了高峰时段充电站的严重拥堵。
在时间维度上,采用逆向规划来探索在车辆保有量、EV 比例、EV 群体电池退化和 PS 变化下的多阶段部署方案。研究了 2025 年至 2045 年山东半岛城市群 EFCS 网络的多阶段部署方案。通过观察EFCS 网络的变化发现,首先,在初始阶段,建设重点是扩大站点的服务覆盖范围,建设对象是主要城市之间的中央道路;其次,随着 EV 城际出行需求的增加,建设重点转向提高关键站点的服务能力,这些站点通常位于主要城市附近。此外,设施利用率在 2035 年至 2045 年间稳定在 0.38 至 0.40 之间,与 2025 年的 0.095 相比有显著提高。随着 EV 城际出行的增加和EFCS 网络的成熟,初始阶段广泛存在的“低利用率”问题得到了解决。在ESER 效益方面,PS 转型在促进交通脱碳方面具有重要意义——网络的实际 GP 比例从 2025 年的 23.7%增加到 2035 年的 47.7%。
在本研究中,规划问题受到简单电力结构(PS)和外部环境变化的限制。未来,PS 中将考虑包括光伏、风能、地热能和核能在内的混合能源。此外,在多阶段规划中应考虑更全面的因素,如渐进式 EV 里程和充电技术。